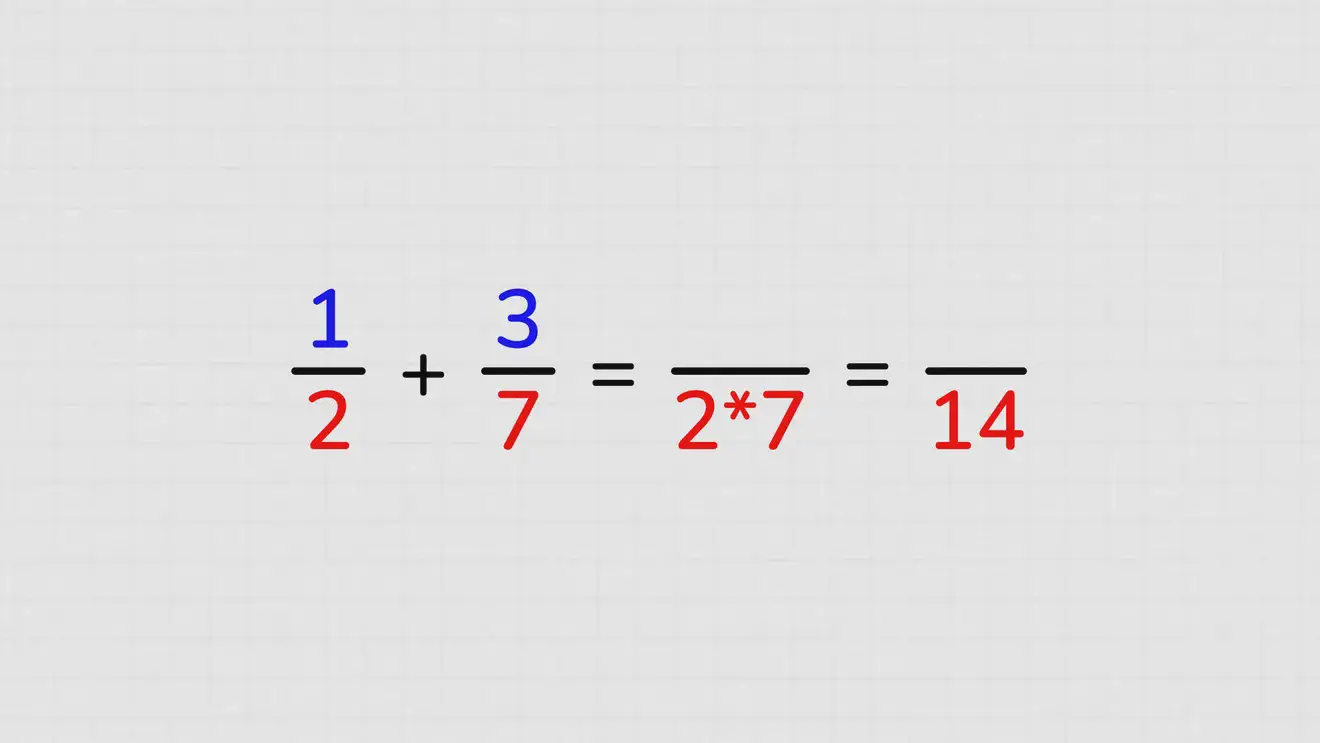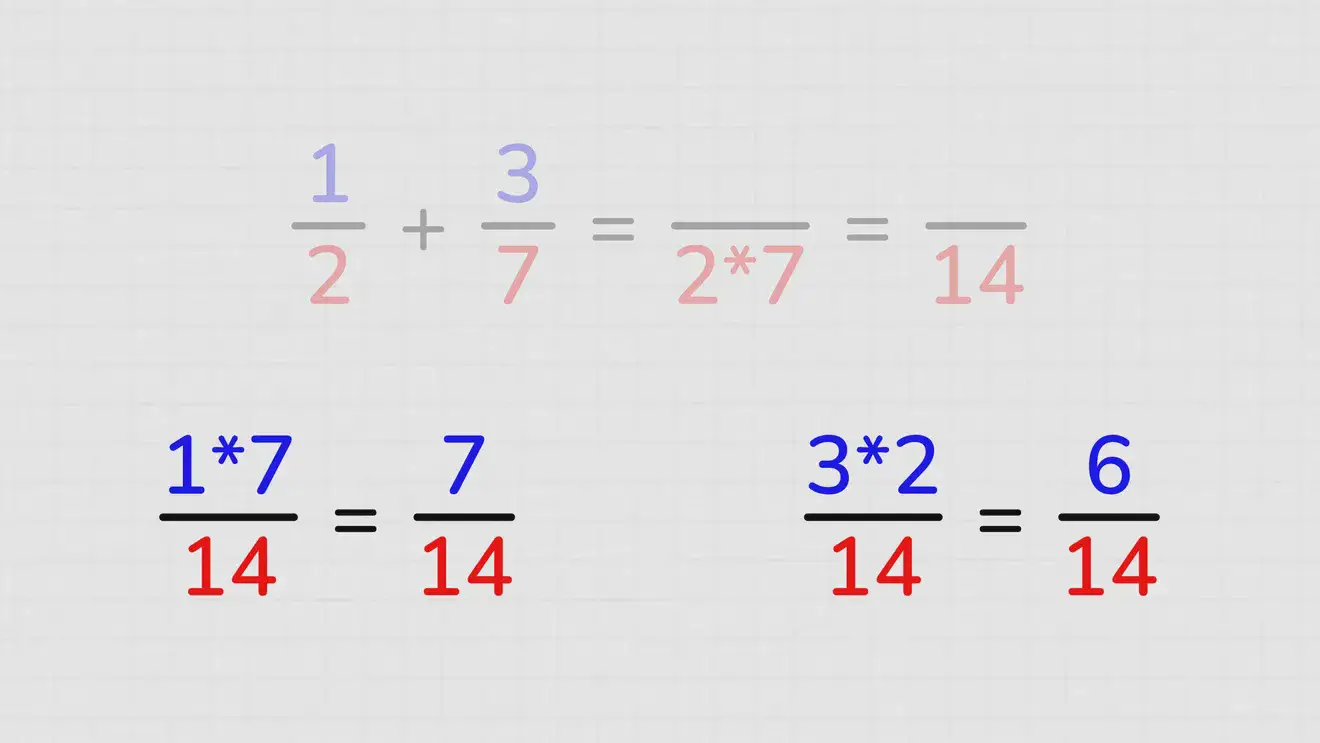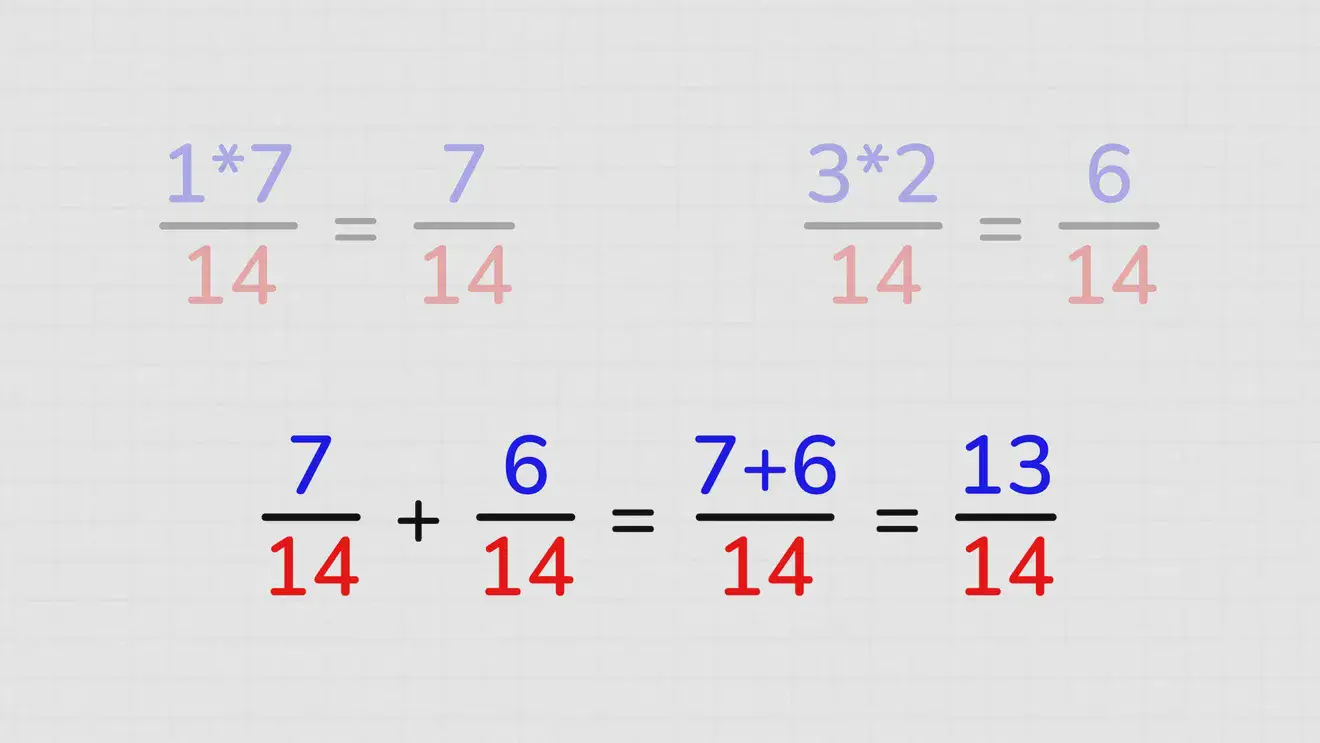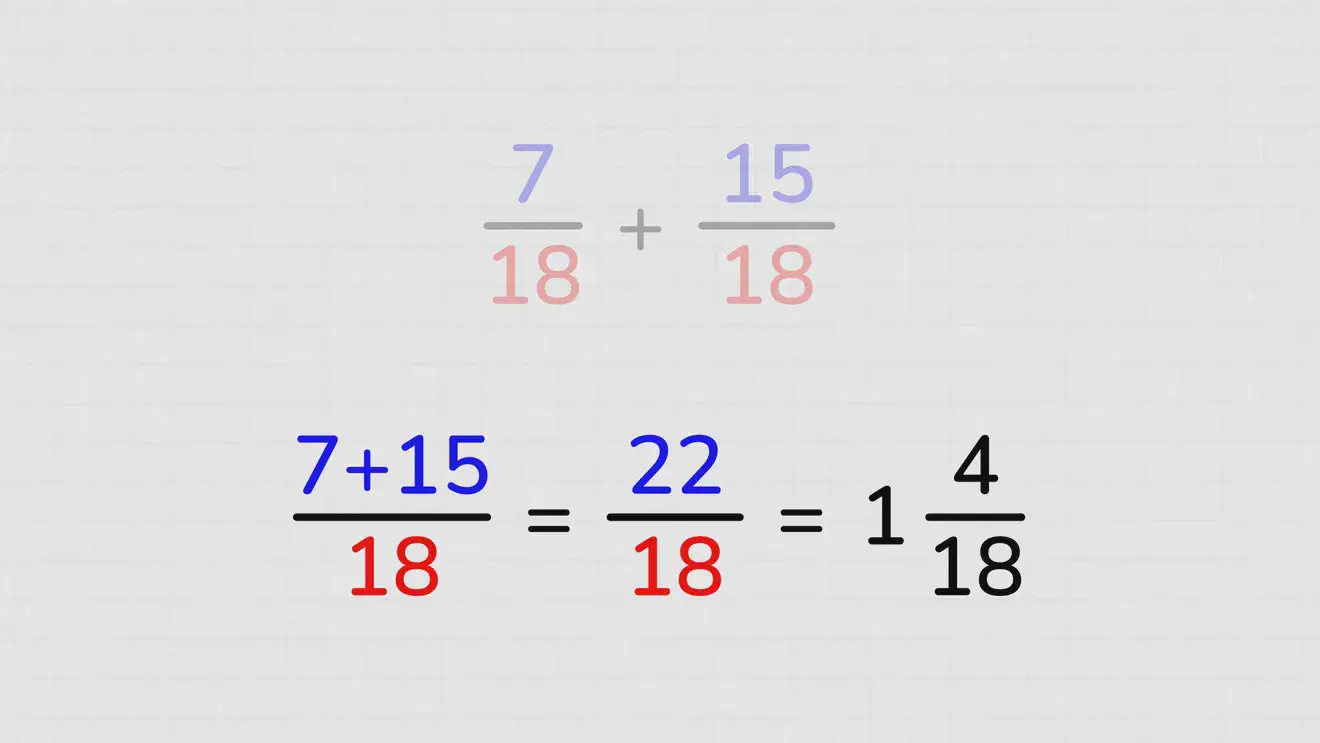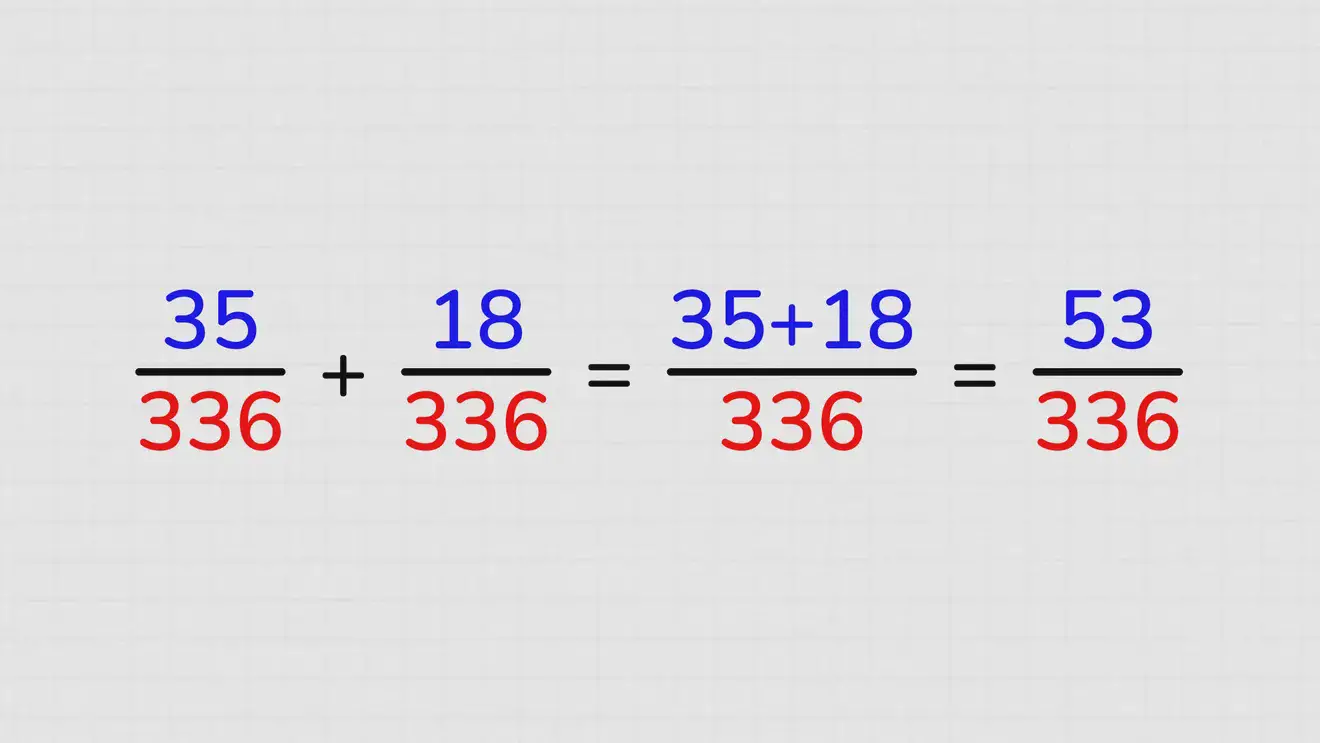Как складывать дроби простые и не очень

Сложение дробных чисел кажется сложным математическим фокусом только тем, кто не знает главный секрет: как дроби с разными знаменателями в несколько действий приводятся к единому знаменателю. Мы раскроем этот секрет и покажем, как использовать новое для вас знание на практике.

Арифметические действия с дробями, как и сами дроби, были введены в научный и практический обиход несколько тысячелетий назад. Это было неизбежно, потому что измерения и вычисления (как абстрактные, так и связанные со строительством, технологиями, торговлей) часто давали в качестве результата помимо целой части числа также и часть меньше единицы. И эту часть необходимо было точно записать и учесть при дальнейших вычислениях и измерениях.

Наиболее привычные сегодня десятичные дроби, которые записываются после целой части числа или нуля, отделяясь от них запятой, далеко не сразу заняли в обиходе господствующее положение. Поначалу все дроби выглядели примерно как сегодняшние обыкновенные дроби: условно чёрточка, обозначающая деление, над ней числитель, под ней знаменатель. И эта старая запись дробей, как и сами недесятичные дроби (например, 1/6 или 3/4), до сих пор широко применяются и в пояснениях к продвинутым исследованиям на экономические или социологические темы, и в строительных или технологических описаниях, и много ещё где. Поэтому умение обращаться с обыкновенными дробями остаётся весьма актуальным. Начнём с приёмов и правил, по которым проводится сложение дробей.

Что такое шипперинг и как его используют фанатыЗачем поклонники сводят любимых персонажей и реальных людей

Что такое дробь

Начнём с азов. Дробь — форма записи нецелого числа. Например, 2/7. Дробь такого типа называется несократимой, потому что не существует числа, на которое можно было бы одновременно разделить и её числитель, и знаменатель.

Другое дело — дробь 4/14. Она сокращаемая: и числитель, и знаменатель можно одновременно разделить на 2, при этом реальный размер записанного числа не изменится. То же самое и при одновременном умножении и числителя, и знаменателя на одно число — величина числа не меняется. Разница только в форме записи.

Пример:

2/7 = (2×3)/(7×3) = 6/21 или

4/14 = (4÷2)/(14÷2) = 2/7

Или, другими словами, 6/21 = 4/14 = 2/7

Это сохранение размера дроби при одновременном умножении или делении и числителя, и знаменателя на одно число называется основным свойством дроби, на котором и основаны правила действия с нецелыми (дробными) числами.

Но правила для дробей с одинаковыми и разными знаменателями имеют отличия.

Как складывать дроби с одинаковыми знаменателями

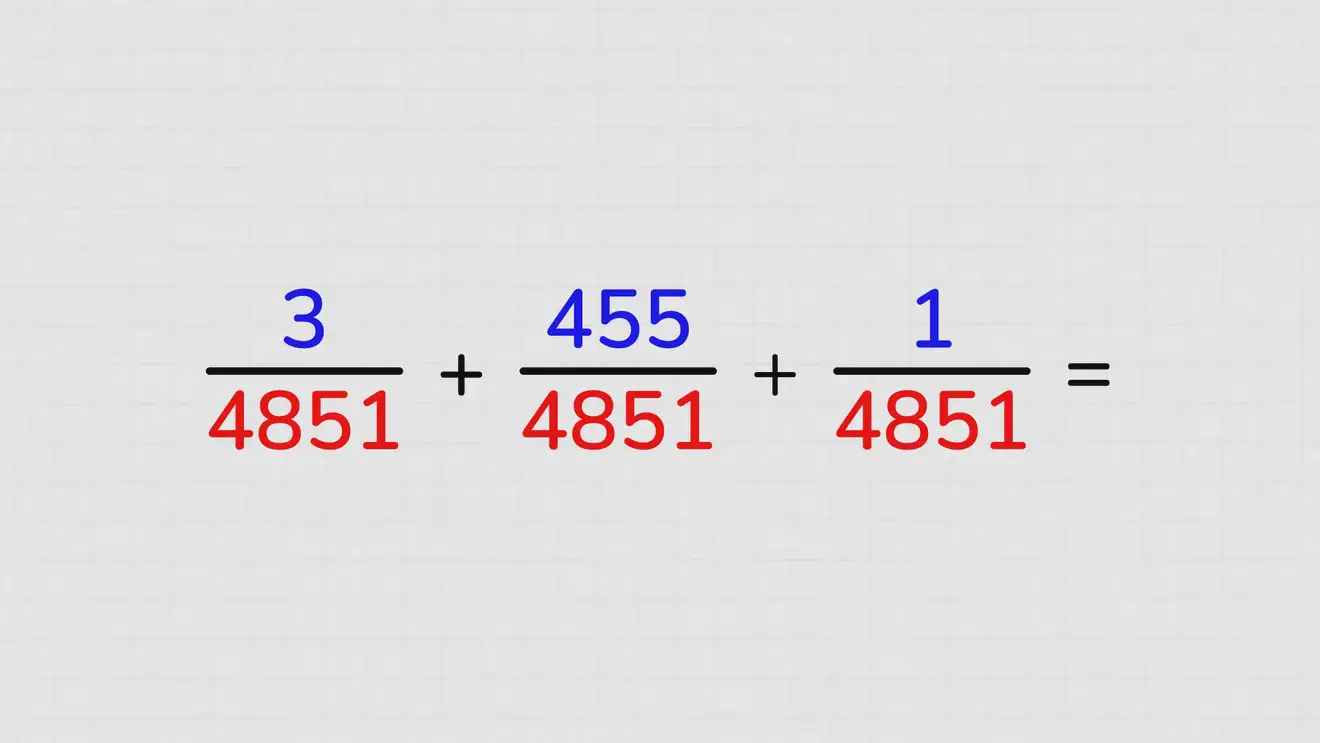
Если возникла необходимость провести сложение дробей, прежде всего нужно посмотреть на их знаменатели — это то, что под чёрточкой. Скажем, дроби 3/4856, 455/4856 и 1/4856 при всём их ужасном виде представляют собой разные количества одинаковых долей — у них один и тот же знаменатель. Их сумму определить просто: нужно сложить числители этих дробей. Знаменатель у итоговой цифры будет тот же, необходимости производить с ним какие-то действия нет.

Пример:

3/4851 + 455/4851 + 1/4851 = (3+455+1)/4856 = 459/4851

@ Изображения: uznay.ru

В этом случае есть смысл упростить получившуюся дробь, разделив и числитель, и знаменатель на 3.

459÷3 = 153, а 4851÷3 = 1671, то есть результат в виде несокращаемой дроби выглядит так: 153/1671. Сокращать дробь есть смысл не только ради более аккуратного вида. Например, если придётся затем складывать её с дробью, у которой другой знаменатель, нужно будет сделать на одну операцию меньше.

Как складывать дроби с разными знаменателями

Если у складываемых дробей разные знаменатели, их приводят к единому знаменателю, а затем умножают их числители в соответствующее число раз (такое же, как знаменатели) и складывают, как в предыдущем примере.

В целом тут возможны несколько вариантов: когда все знаменатели — простые числа, когда знаменатели — взаимно кратные числа, и когда каждый из знаменателей кратен нескольким числам сразу.

В первом случае, когда знаменатели это простые числа (2, 3, 5, 7, 11 и т.д.), то есть ни на какое число не делятся, выход один: получить единый знаменатель перемножением знаменателей дробей.

Пример:

Нужно сложить 1/2 и 3/7.

Общий знаменатель будет 2×7=14. Но тогда числитель первой дроби также надо увеличить на 7, и первая дробь станет выглядеть как 7/14. Числитель второй дроби нужно, как и знаменатель, умножить на 2. Вторая дробь станет выглядеть как 6/14.

Когда найден общий знаменатель, останется провести действия, как с дробями с одинаковым знаменателем. 7/14+6/14= (7+6)/14= 13/14.

@ Изображения: uznay.ru

Второй случай простой: если один знаменатель кратен другому (делится на него), не надо для поиска общего знаменателя перемножать знаменатели.

Пример:

Нужно сложить 7/18 и 5/6.

Первый знаменатель, 18, явно получается из умножения второго, 6, на 3. Таким образом, с первой дробью ничего делать не надо. Вторую, чтобы она получила общий знаменатель с первой, надо изменить, помножив её обе части (выше чёрточки и ниже) на 3. То есть (5×3)/(6×3)= 15/18.

Для определения результата складывается 7/18 и 15/18. (7+15)/18=22/18

Результат — неправильная дробь, у неё числитель больше знаменателя. Лучше её привести в вид смешанного числа (смешанной дроби), состоящего из целой и дробной частей – 1 4/18.

@ Изображения: uznay.ru

Третий вариант отличается от предыдущих тем, что в нём каждый из знаменателей складываемых дробей кратен нескольким числам. На основании этих чисел определяется наименьший общий знаменатель (его называют НОК — наименьшее общее кратное). Он так называется, потому что является числом меньшим, чем просто произведение знаменателей складываемых дробей, причём наименьшим из тех, из тех, которые могли бы стать общим знаменателем. Этот минимализм понятен: представьте, что простых дробей складывается не две, а пять, и у каждой двузначный знаменатель.

Начинается определение НОК с выяснения, перемножением каких чисел являются знаменатели складываемых дробей.

Пример:

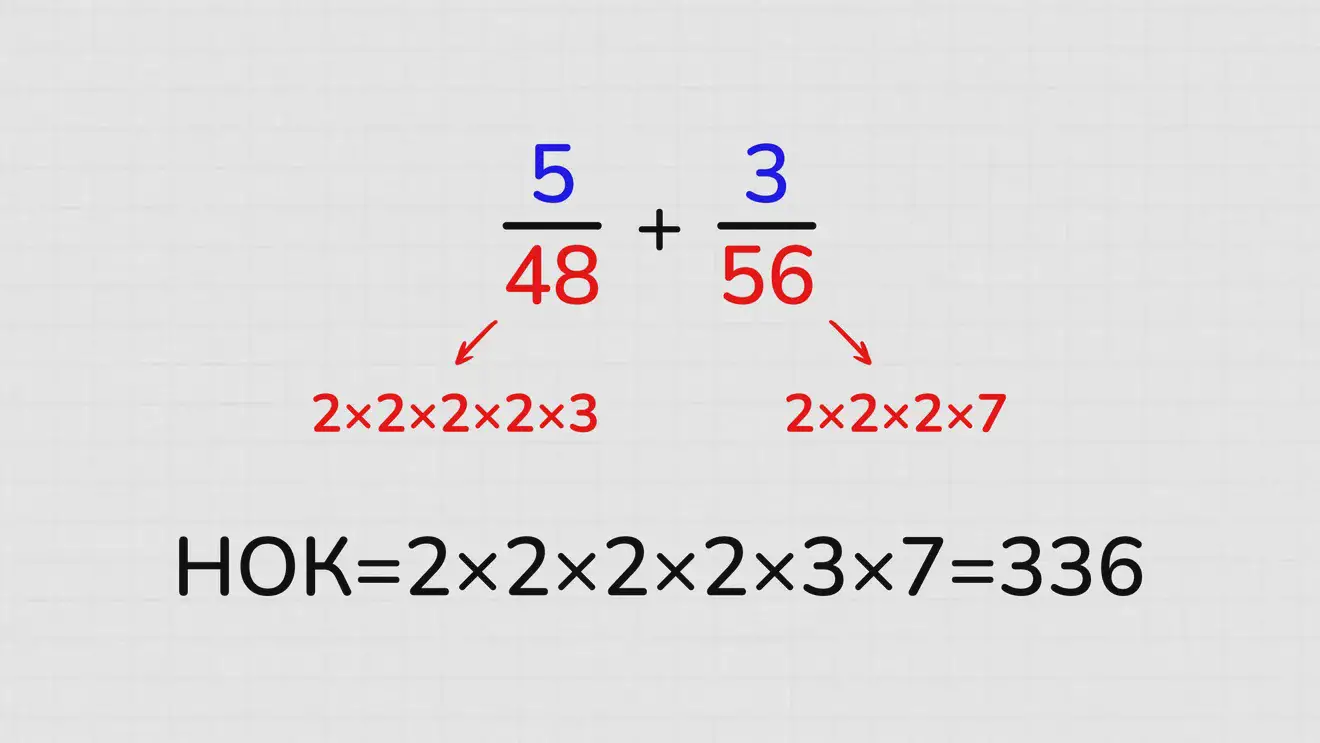
Нужно сложить 5/48 и 3/56.

Определение НОК

Выясняем, из чего «состоит» число 48, подбирая ему очевидные делители. Сначала это 2, затем опять 2 (24 тоже делится на 2), затем вновь 2, ещё раз 2, и в заключение 3 (после деления 6 на 2 осталось 3, которое делится только само на себя). 48=2×2×2×2×3. Аналогично разбираем 56. 56=2×2×2×7. НОК получается от перемножения найденных составляющих, исключая «дубли»: то есть двойки включаются только из первого числа, их там больше, от второго пригодится только семёрка. НОК для 48 и 56 оказывается равен 2×2×2×2×3×7=336.

Приведение к общему знаменателю

 Чтобы узнать, насколько нужно увеличить числитель и знаменатель первой дроби, 5/48, делим 336 на 48. Получается 7. Значит, новая запись дроби, уже приведённой к НОК, будет (5×7)/(48×7)=35/336. Делитель для второй дроби, 3/56, определённый аналогично, 6. Её новый вид: (3×6)/(56×6)=18/336.

Результат: 35/336+18/336=(35+18)/336=53/336.

@ Изображения: uznay.ru

Как складывать смешанные дроби

Смешанные дроби — это числа, состоящие из целой части и дробной. Они также могут быть представлены в виде дроби, числитель которой больше, чем знаменатель. То есть это числа вида 1½, которые можно записать и как 3/2. Для случаев, когда нужно сложить смешанные дроби, чтобы не усложнять вычисления, сначала складываются отдельно целые части, затем дробные.

Пример:

Нужно сложить 1½ и 1½.

Сначала складываются целые части (1+1)=2 , затем этот результат добавляют к сумме дробных частей. 2+(½+½) = 2+1=3.

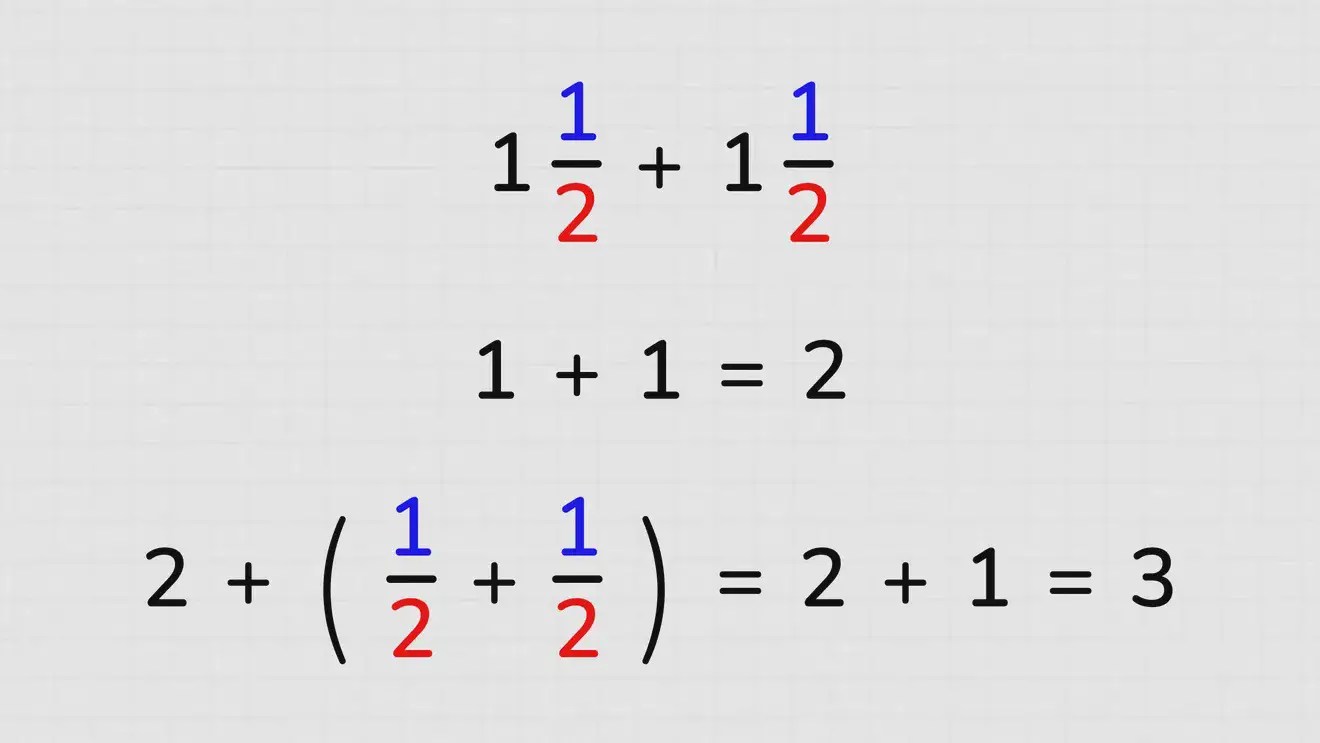
Как складывать десятичные дроби

У десятичных дробей другая система запиcи — позиционная. Поэтому приёмы, используемые для операций с простыми дробями, для них не используются. Дроби вида 0,385 удобны для подсчётов «в столбик», потому что место, которое занимает цифра после запятой, упрощает вычисление до простейшего арифметического действия.

При этом любую простую дробь можно преобразовать, если нужно, в десятичную. А десятичную — в простую. Число, приведённое в качестве примера, может быть представлено и так — 385/1000. Однако так имеет смысл делать разве что в случае, когда десятичные дроби необходимо сложить с простыми и представить результат в виде простой дроби.