Как найти сторону треугольника

В школе на уроках геометрии очень часто приходится иметь дело с треугольниками, а самая распространённая задача — нахождение их элементов, в частности, сторон, по другим известным параметрам. Рассмотрим различные варианты решения таких задач в зависимости от исходных данных.

Общие случаи

Известен периметр и 2 стороны

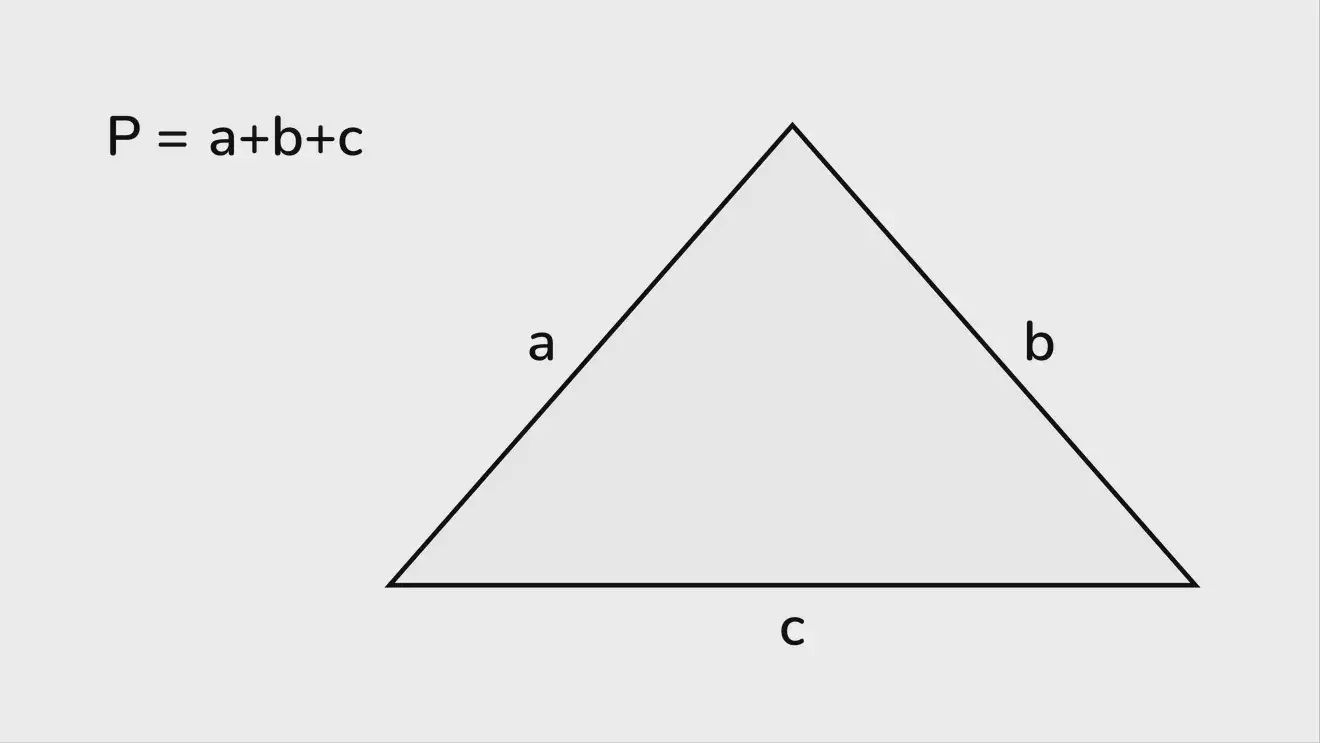
Периметр (P) — это сумма длин всех сторон.

Следовательно, чтобы найти неизвестную сторону, необходимо вычесть из периметра две заданных:

a = P − (b+c).

Известны площадь и высота

Высота — отрезок, проведённый из вершины треугольника к одной из его сторон под углом 90°.

Зная площадь треугольника и высоту, можно найти сторону, к которой она проведена, используя формулу площади:

Врач Горячев: при измерении давления надо учитывать, какая рука является ведущейКак получить точные результаты при измерении артериального давления

S = ½·a·h, где h — высота, S — площадь.

Выразив отсюда неизвестную сторону, получим:

a = 2·S/h.

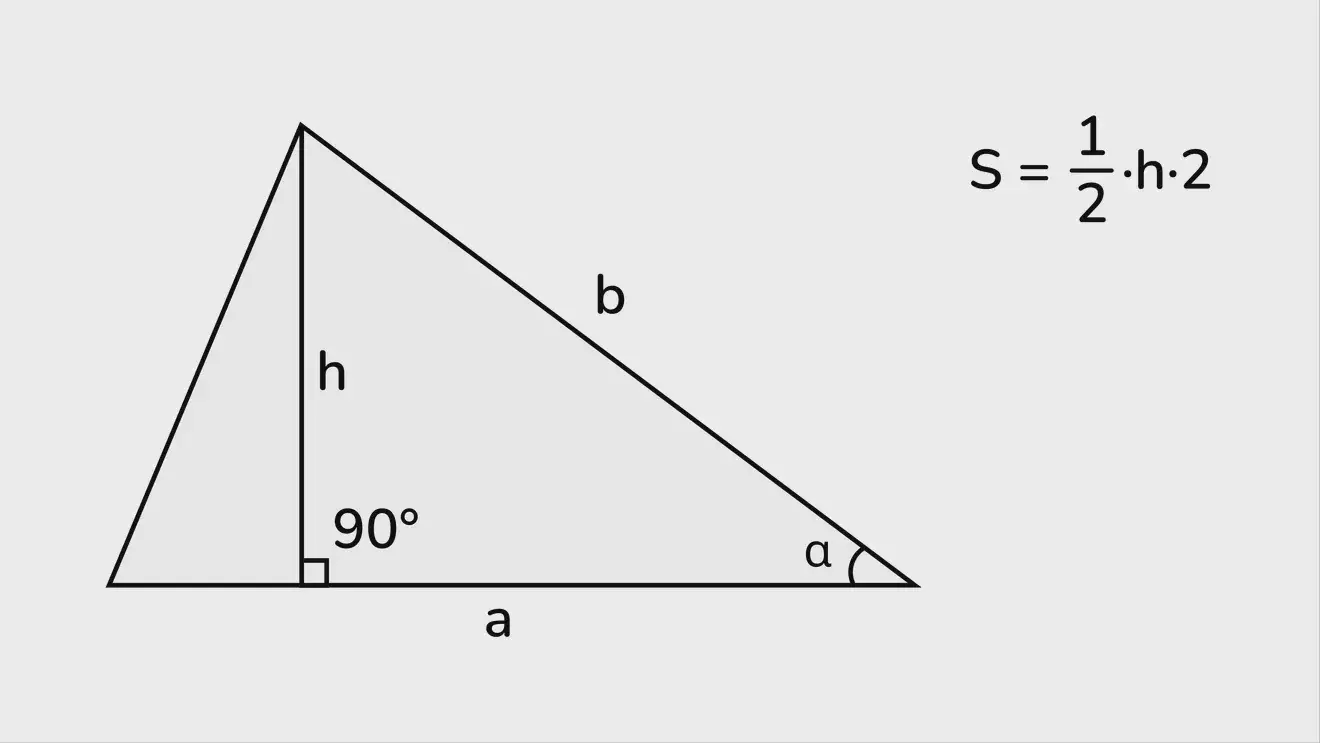
Примечание: если высота не задана, но известны другая сторона и угол между ней и искомой, то высоту можно найти через синус этого угла:

h = b·sin(α).

И если подставить это выражение в полученную выше формулу, она приобретает вид:

a = 2·S/(b·sin(α)).

Пример

Дано:

S = 5, b = 4, α = 30°.

Решение:

h = b·sin (α) = 4·sin (30) = 4·½ = 2;

a = 2·S/h = 2·5/ 2= 5.

Известны 2 стороны и угол между ними

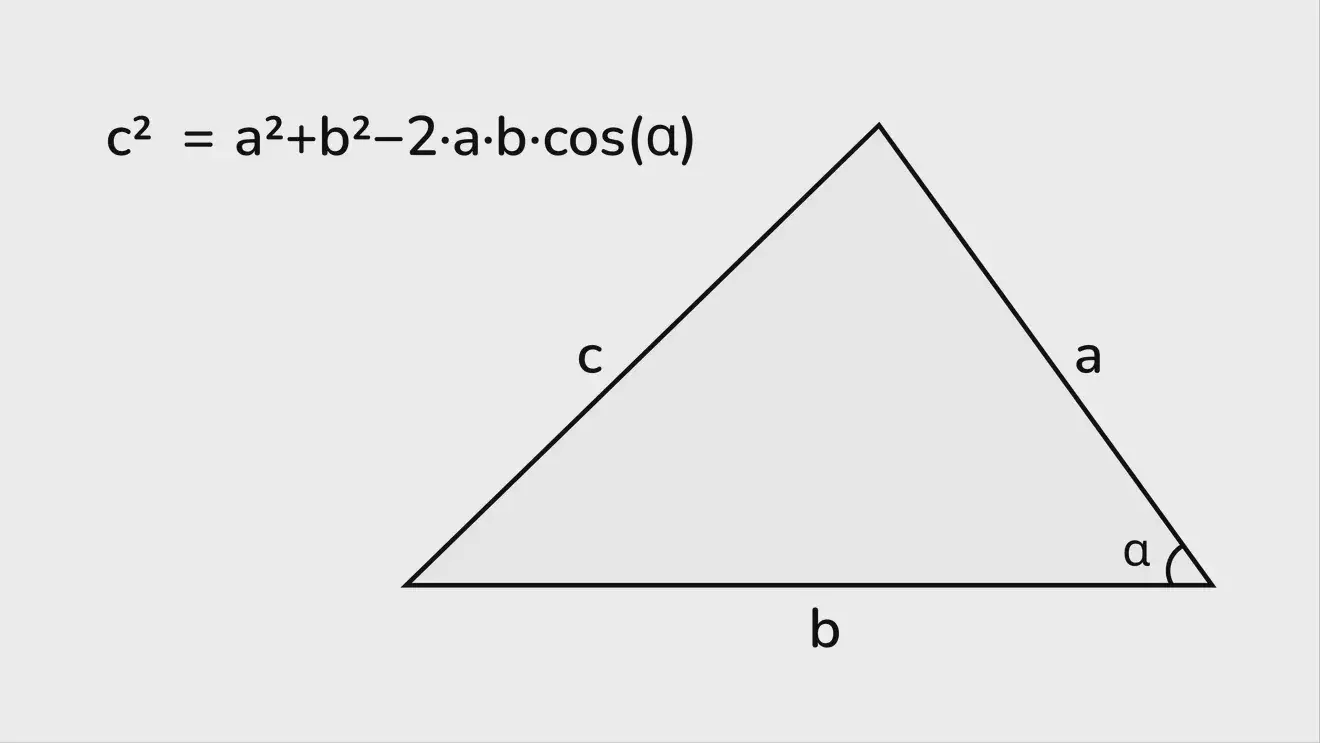
Стороны треугольника связаны между собой теоремой косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

В формульном виде равенство записывается как

c² = a²+b²−2·a·b·cos(α),

то есть неизвестную сторону с можно найти, если извлечь квадратный корень из этого выражения.

Пример

Дано:

а = 5, b = 10, α = 60°.

Решение:

c = √(a²+b²−2ab·cos(α)) = √(5²+10²−2·5·10·cos(60)) = √(25+100−100·½) = √75 = 5√3.

Известны 2 угла и сторона

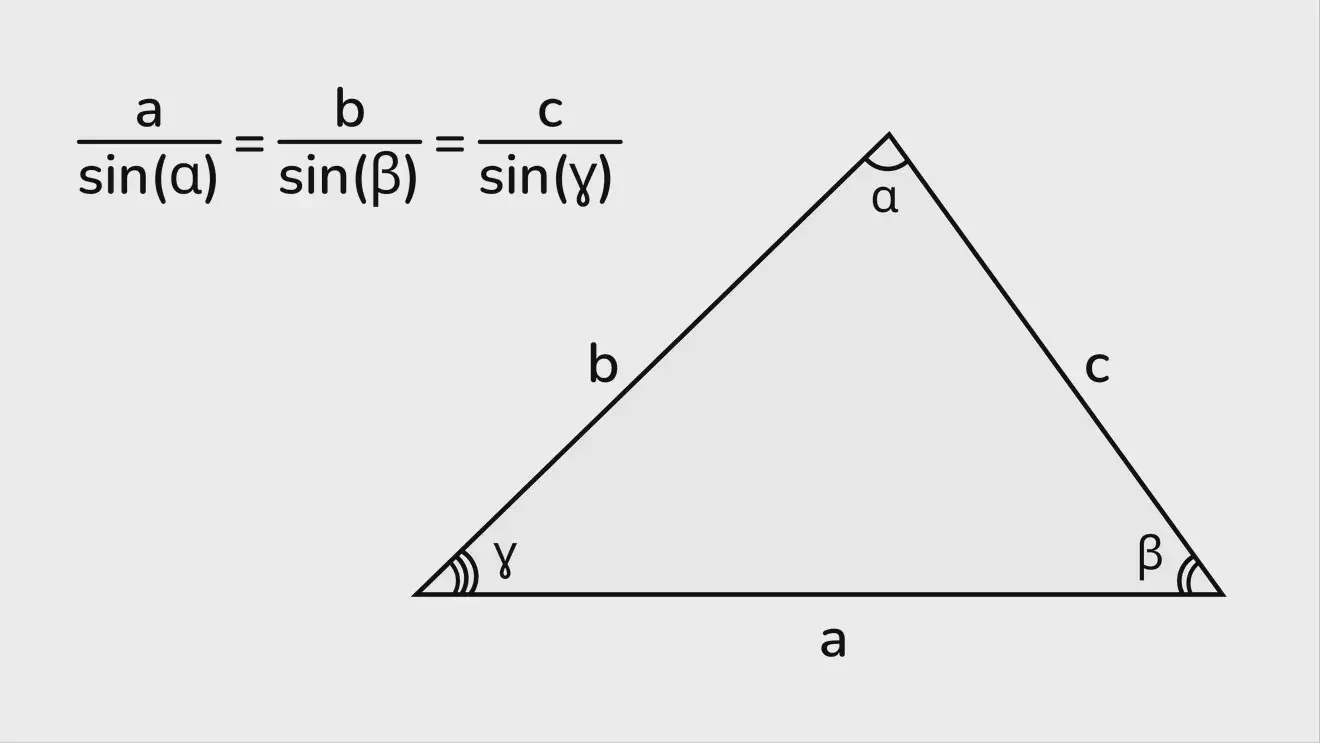
Теорема синусов гласит, что стороны треугольника пропорциональны синусам противолежащих им углов:

a/sin(α) = b/sin(β) = c/sin(ɣ).

Соответственно, в зависимости от конкретных исходных данных можно выразить искомую сторону:

a = b·sin(α)/sin(β) или a = c·sin(α)/sin(ɣ);

b = a·sin(β)/sin(α) или b = c·sin(β)/sin(ɣ);

c = a·sin(ɣ)/sin(α) или c = b·sin(ɣ)/sin(β).

Пример

Дано:

b = 10, α = 45°, β = 30°.

Решение:

a = b·sin(α)/sin(β) = 10·(√2/2):(½) = 10·(2√2)/2 = 10√2.

Известен противолежащий угол и радиус описанной окружности

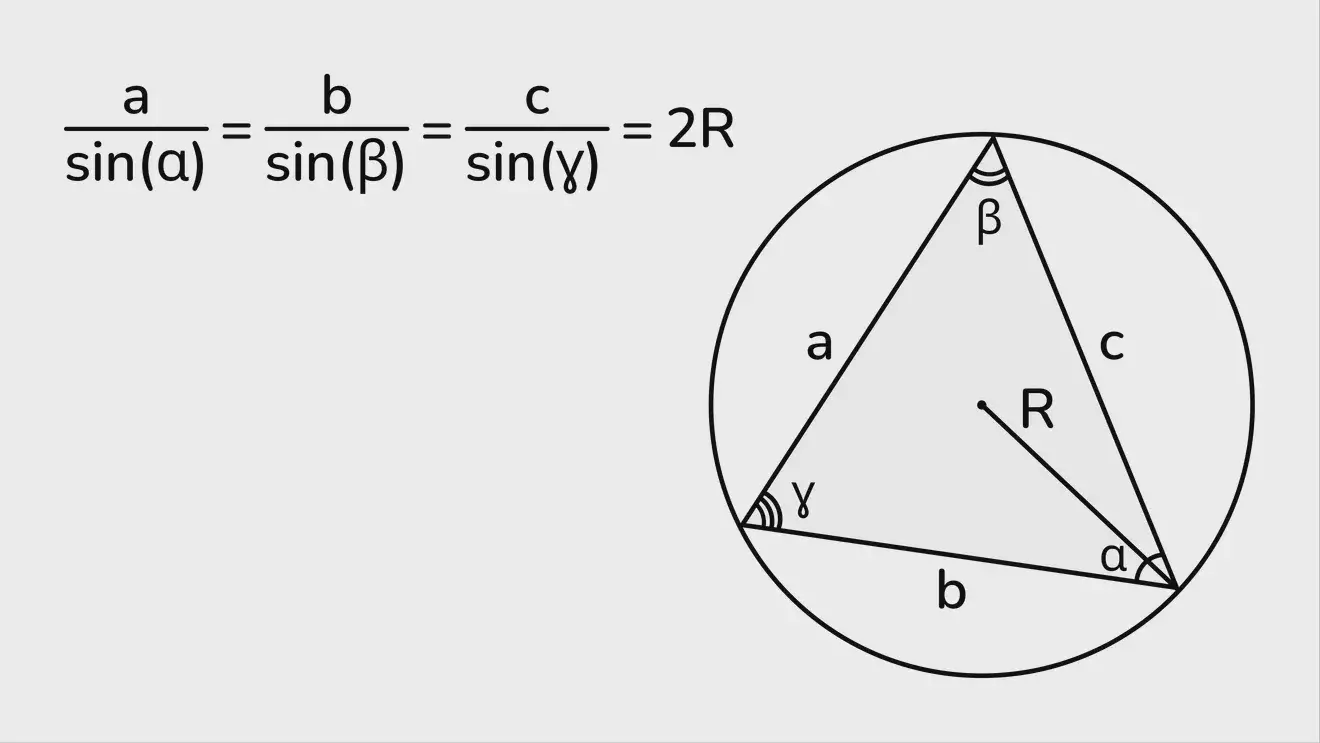
Существует расширенная теорема синусов, устанавливающая связь между отношениями сторон к противолежащим углам и радиусом окружности, описанной вокруг треугольника:

a/sin(α) = b/sin(β) = c/sin(ɣ) = 2R.

Тогда стороны можно представить как

a = 2·R·sin(α);

b = 2·R·sin(β);

a = 2·R·sin(ɣ).

Частные случаи

Прямоугольные треугольники

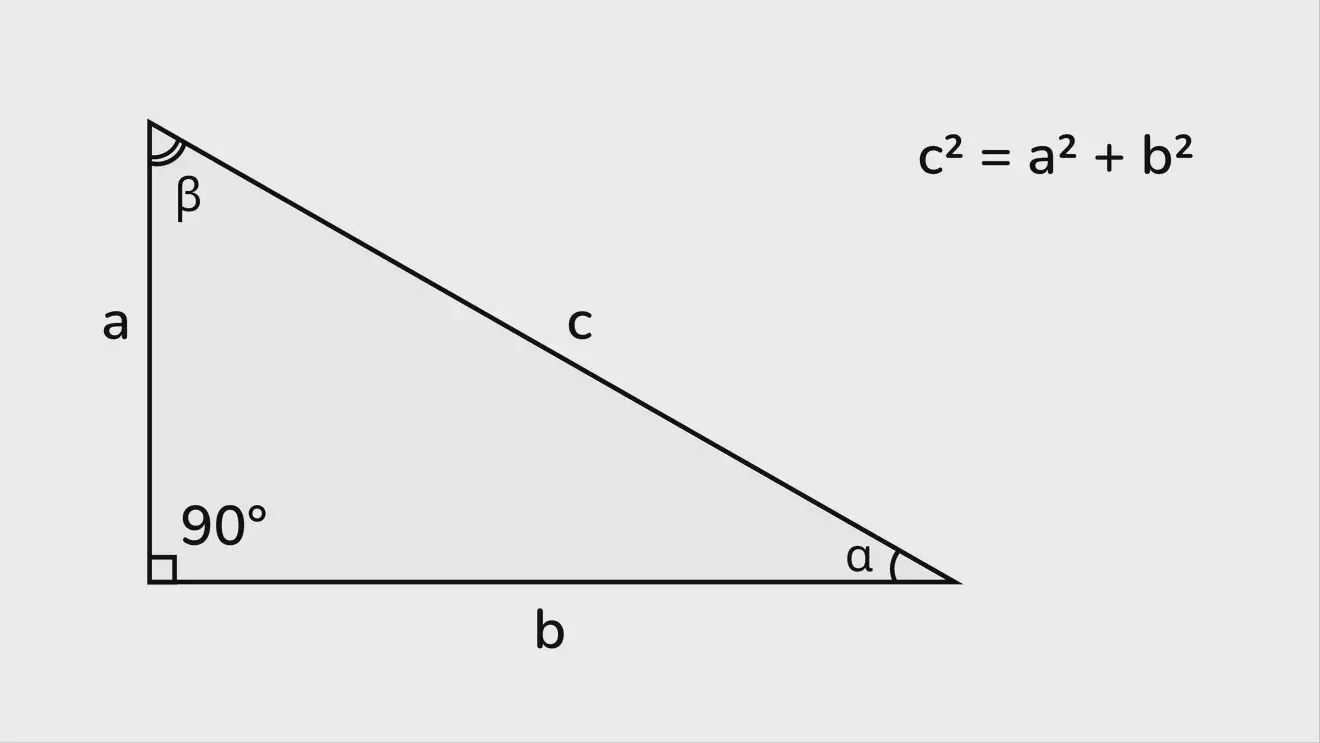
Теорема Пифагора

Теорема Пифагора — частный случай теоремы косинусов.

Поскольку cos(90°) = 0, то последнее слагаемое (удвоенное произведение сторон) сокращается, и выражение преобразуется в привычное всем со школьной скамьи «квадрат гипотенузы равен сумме квадратов катетов»:

c² = a² + b².

Отсюда можно найти гипотенузу

c = √(a² + b²),

а также катеты

a = √(c² − b²) и b = √(c² − a²).

Тригонометрические функции

Тригонометрия вводит понятия синуса, косинуса, тангенса и котангенса — отношения сторон прямоугольного треугольника относительно его углов:

sin(α) = a/c;

cos(α) = b/c;

tg(α) = a/b;

ctg(α) = b/a.

Кроме того, не стоит забывать, что сумма углов треугольника равна 180°, а поскольку известно, что один из углов прямой, то два оставшихся связаны выражением α+β=90°.

Таким образом, зная в прямоугольном треугольнике всего лишь 1 любой угол и 1 любую сторону, можно найти все остальные элементы:

α = 90 − β или β = 90 − α;

a = c·sin(α) или a = b·tg(α);

b = c·cos(α) или b = a·ctg(α);

c = a/sin(α) или c = b/cos(α).

Пример 1

Дано:

в прямоугольном треугольнике a = 4, α = 30°.

Решение:

b = a·ctg(α) = 4·ctg(30) = 4√3;

c = a/sin(α) = 4:½ = 4·2 = 8.

Пример 2

Дано:

в прямоугольном треугольнике b=4, S=6.

Решение:

катет прямоугольного треугольника является одновременно и его высотой, проведённой к другому катету.

Значит справедлива формула из пункта про площадь и высоту

a = 2·S/h, где h=b.

Тогда a = 2·S/b = 2·6/4 = 3, а гипотенузу найдём по теореме Пифагора:

c = √(a²+b²) = √(3²+4²) = √25 = 5.

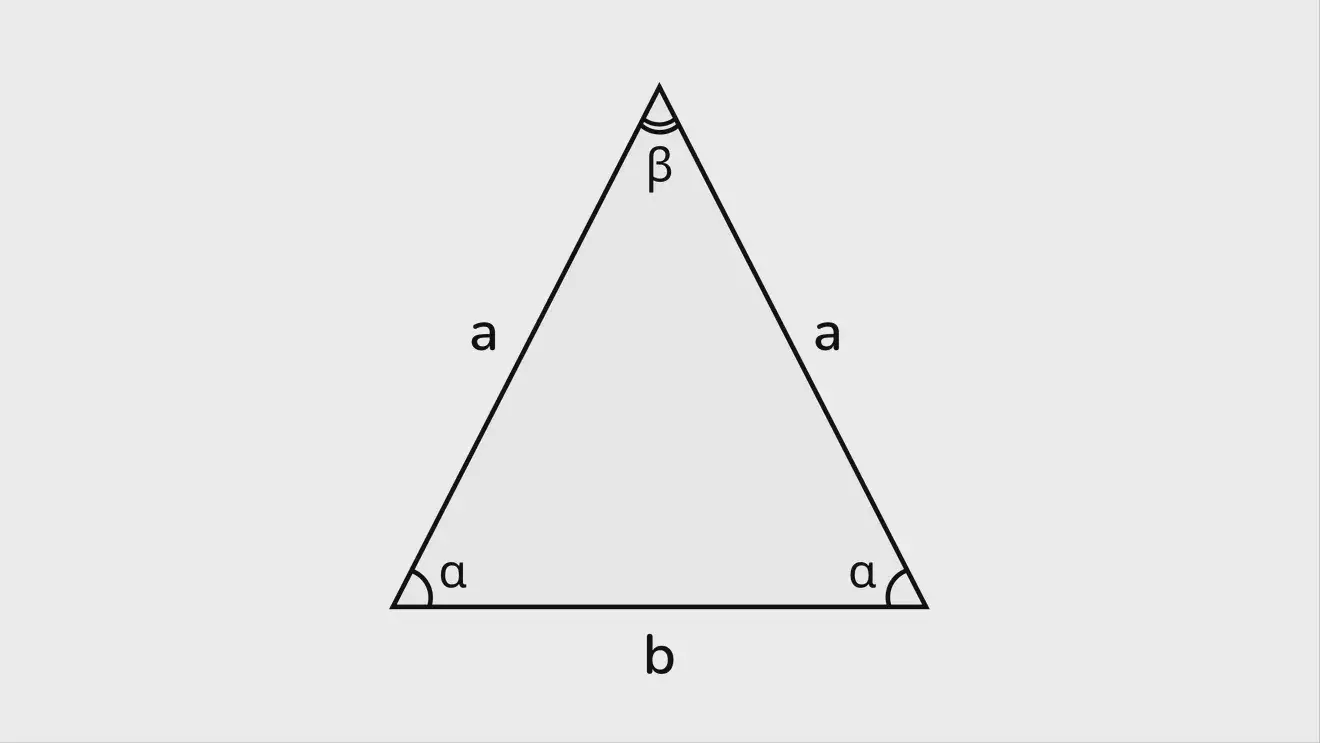
Равнобедренные треугольники

В равнобедренном треугольнике равны углы при основании и две других стороны («бедра»), что может значительно облегчить расчёты по общим формулам.

К примеру, теорема косинусов упростится до b = a·√(2−2cos(β)).

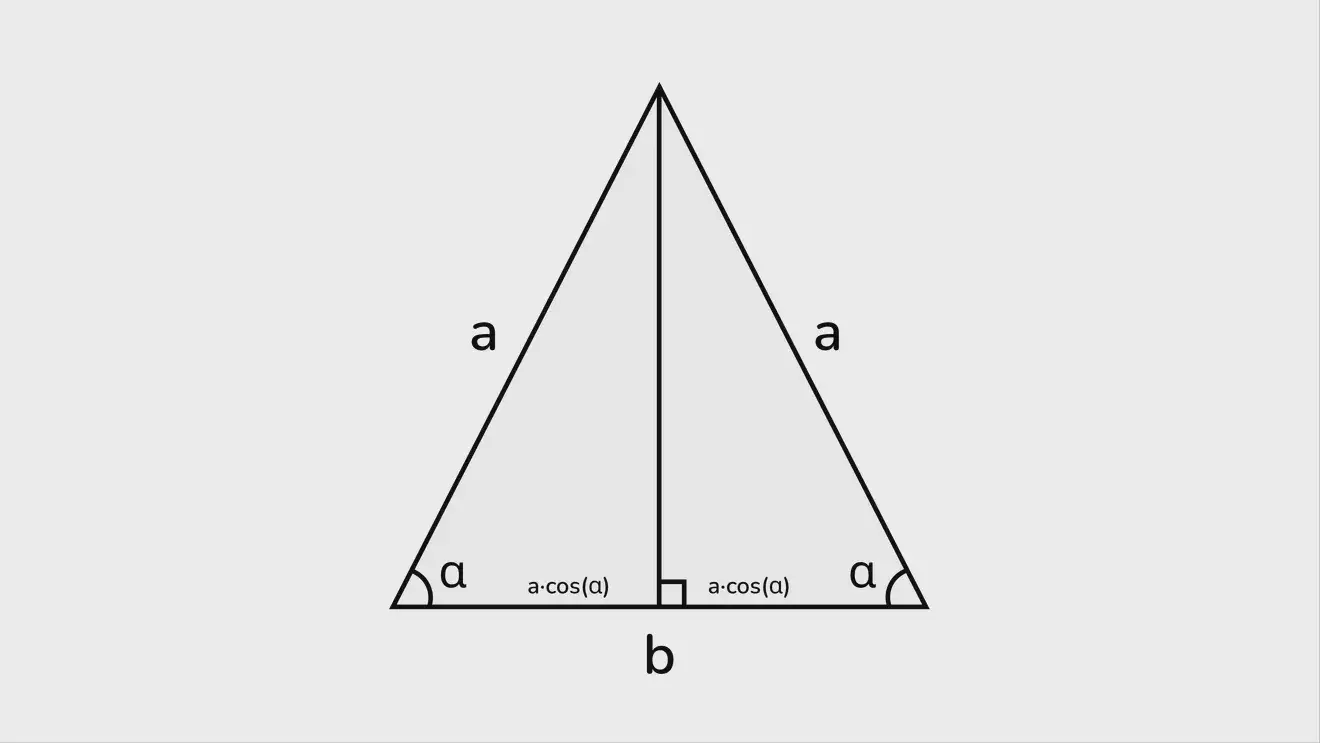
Также основание можно найти тригонометрическими формулами, проведя высоту и воспользовавшись полученными 2 прямоугольными треугольниками:

 b = 2·a·cos(α).

Если известно основание, то бёдра можно выразить из формул выше:

a = b/√(2−2cos(β)) или a = b/2cos(α).

А если даны площадь и угол между равными сторонами, можно использовать формулу площади равнобедренного треугольника: S = ½ a²⋅sin(β), откуда

a = √(2·S/sin(β)).

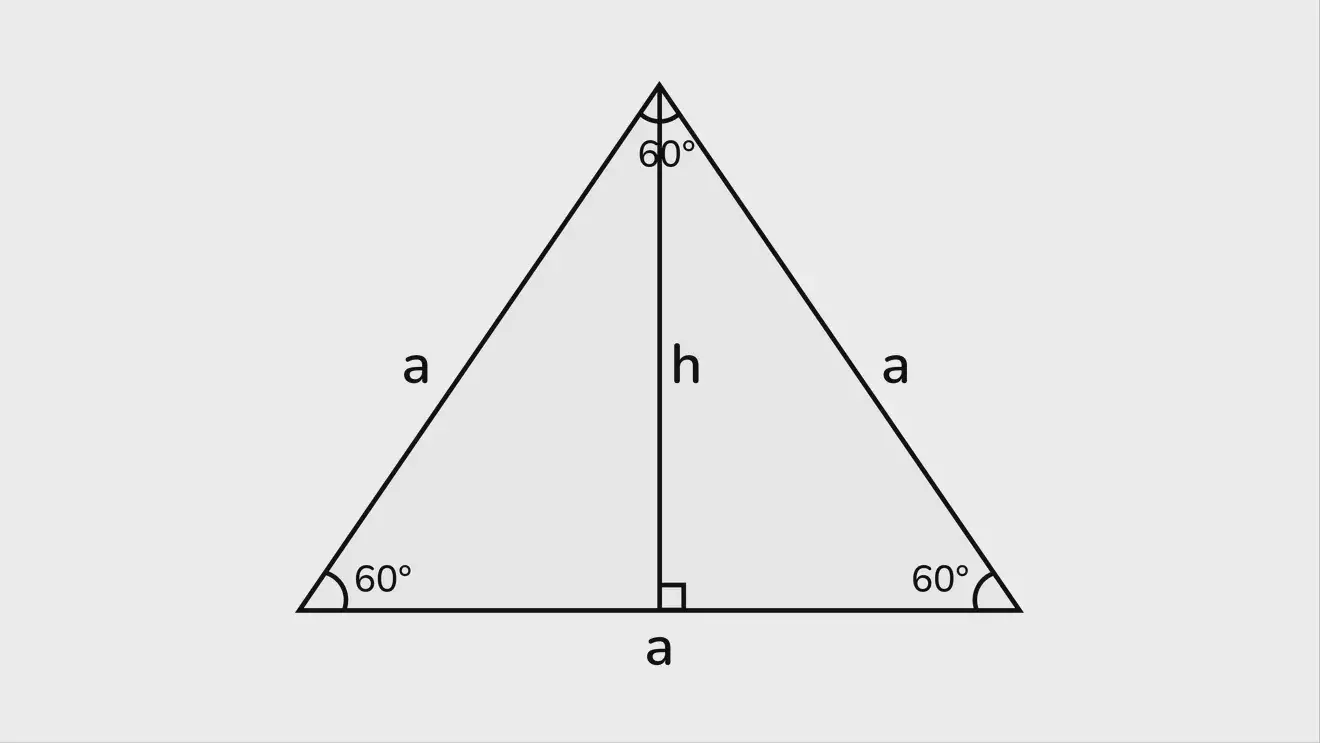
Равносторонние треугольники

Как можно понять из названия, в равносторонних треугольниках равны все стороны, а все углы всегда составляют 60°. Это ещё сильнее упрощает все возможные формулы.

Например, зная высоту, можно легко найти сторону через синус угла:

a = h/sin(60°) = 2h/√3.

Либо, если дана площадь, можно упростить формулу для равнобедренного треугольника, благодаря известным углам:

S = ½ a²⋅sin(β) = ½ a²⋅sin(60) = a²√3/4, откуда

a = 2√(S/√3)).

Полезные сервисы

Если самостоятельное вычисление вызывает затруднения или на него не хватает времени, можно прибегнуть к помощи онлайн-калькуляторов.

Один из наиболее полных и удобных — сайт MathWeb.

Чтобы получить решение задачи:

— найдите пункт «Сторона треугольника» в разделе «Стороны фигур»;

— выберите тип треугольника;

— введите все известные данные прямо на рисунке;

— нажмите кнопку «Вычислить».

Если введённых значений достаточно для вычисления, калькулятор выдаст расчёт всех элементов треугольника вместе с используемыми формулами, что очень полезно при выполнении домашнего задания. 

Кроме того, несомненным плюсом этого сайта является неограниченное бесплатное использование, а также подробность решения.