Как найти площадь треугольника методами геометрии

Вычисление площади треугольника — задача, вполне востребованная в реальной жизни: практически любая фигура, ограниченная прямыми линиями, — это комбинация прямоугольников и треугольников. И если с первыми всё понятно — надо длину помножить на ширину, то со вторыми посложней. О способах найти площадь любых треугольников при минимуме данных мы и расскажем.

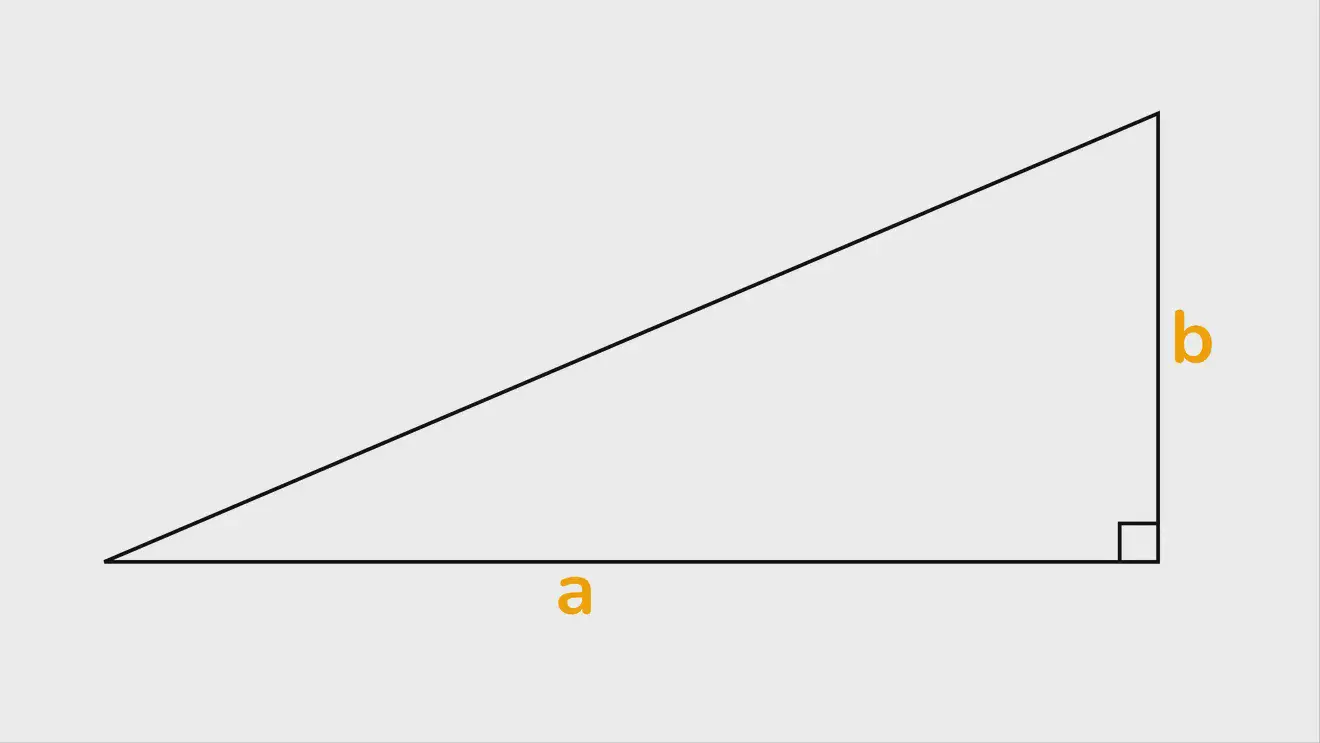
Основной способ найти площадь треугольника

В основе всех формул расчёта площади треугольников один метод — для прямоугольного треугольника. Длины сторон, образующих прямой угол (катеты), перемножаются, а потом полученное делится пополам. Отсюда главная формула:

S(площадь)= ½ × а(первый катет)× b (второй катет).

Но в задачниках и на практике треугольники бывают не только прямоугольные, а размер их сторон или величина углов зачастую неизвестны. В таких случаях недостающие данные определяются с помощью значений тригонометрических функций cos, sin, tg и ctg (эти значения определяются на калькуляторе). Так сложилось, что для упрощения вычислений все варианты задач разделены по объёму исходных данных, и для них определены соответствующие формулы.

Врач Горячев: при измерении давления надо учитывать, какая рука является ведущейКак получить точные результаты при измерении артериального давления

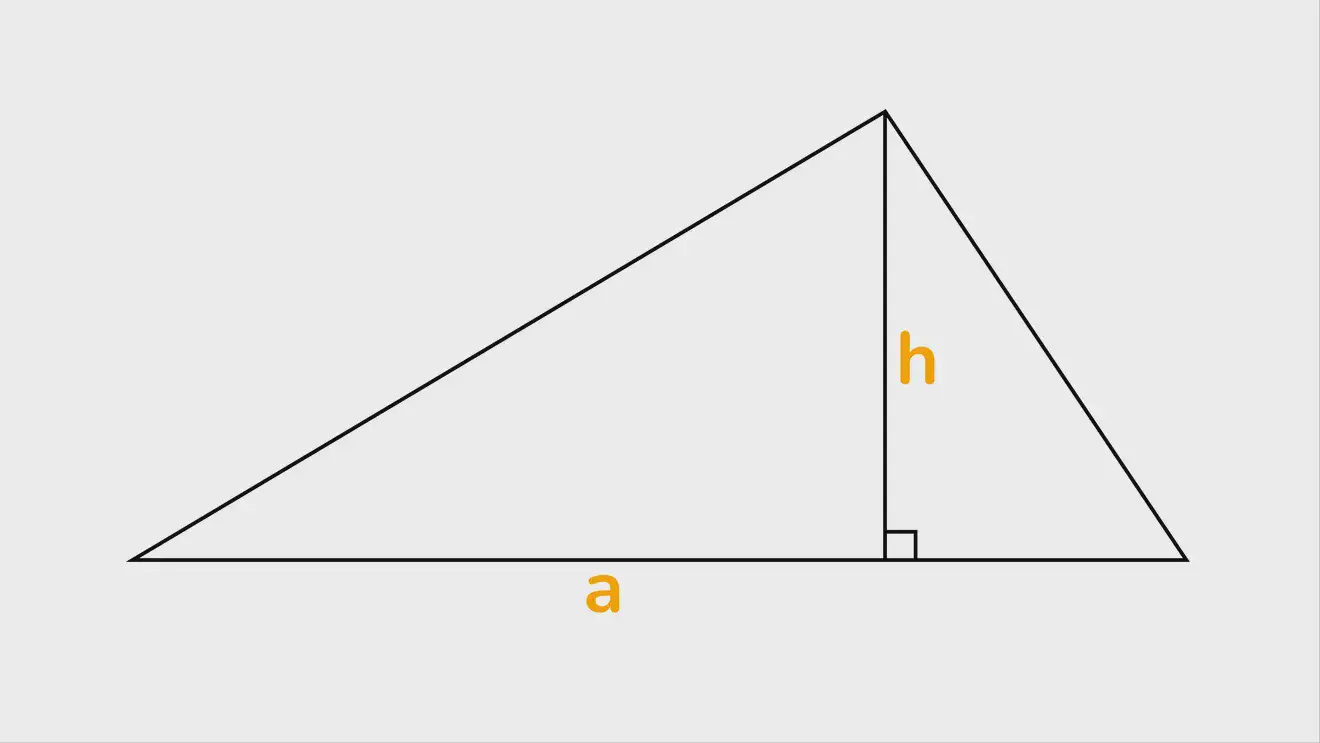
Если известна одна из сторон и построенная от неё высота

Высота проведена под прямым углом от одной из сторон (основания) и упирается в расположенный напротив неё угол. Фактически получаем 2 смежных прямоугольных треугольника, у которых известна длина 1 катета — это высота, и сумма длин 2 других катетов.

S=1/2⋅a⋅h (h — высота, a — сторона, от которой она построена)

По сути, это частный случай главной формулы.

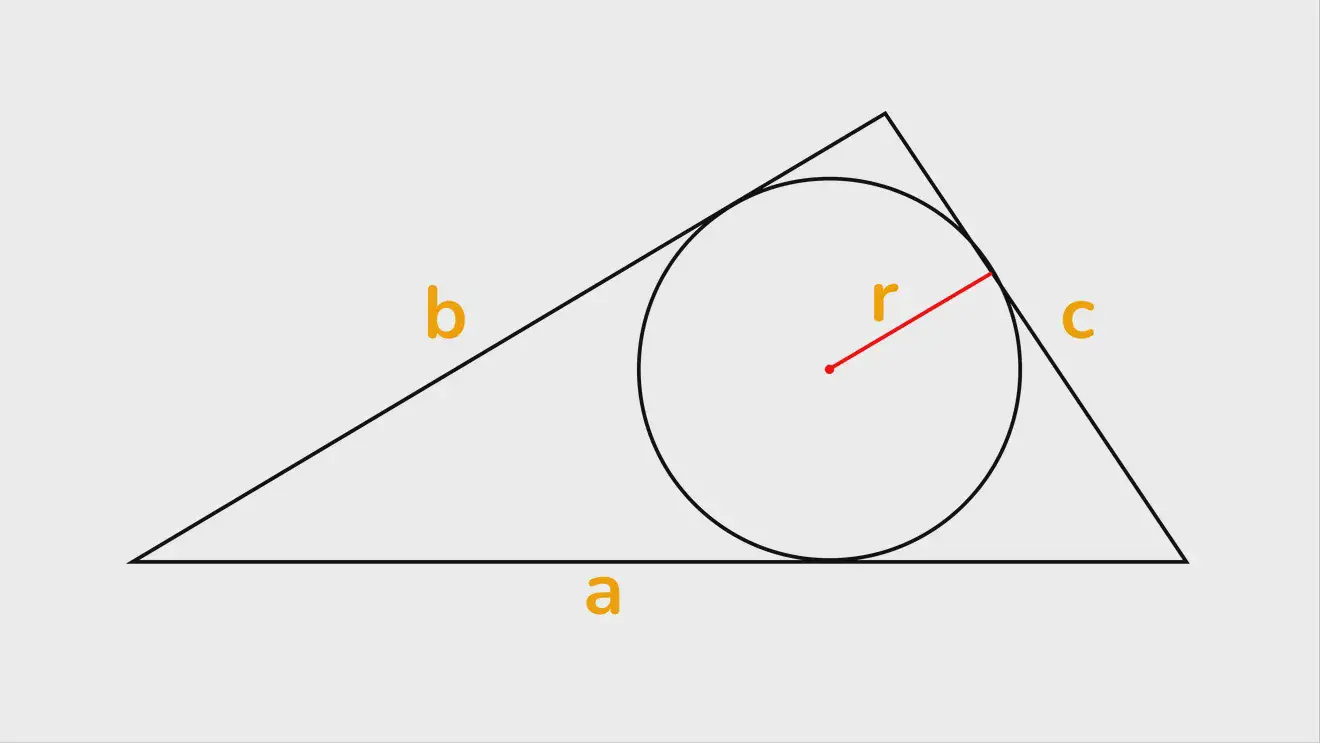
Если известны стороны треугольника и радиус вписанной в него окружности

Это усложнённый случай предыдущего варианта. Радиус, проведённый из точки касания окружности со стороной, здесь заменяет высоты для 3 виртуальных треугольников с вершинами в центре окружности. Площадь — сумма площадей 3 виртуальных треугольников. При сторонах a, b и c и высоте r получается:

S=1/2⋅r⋅(a+b+c)

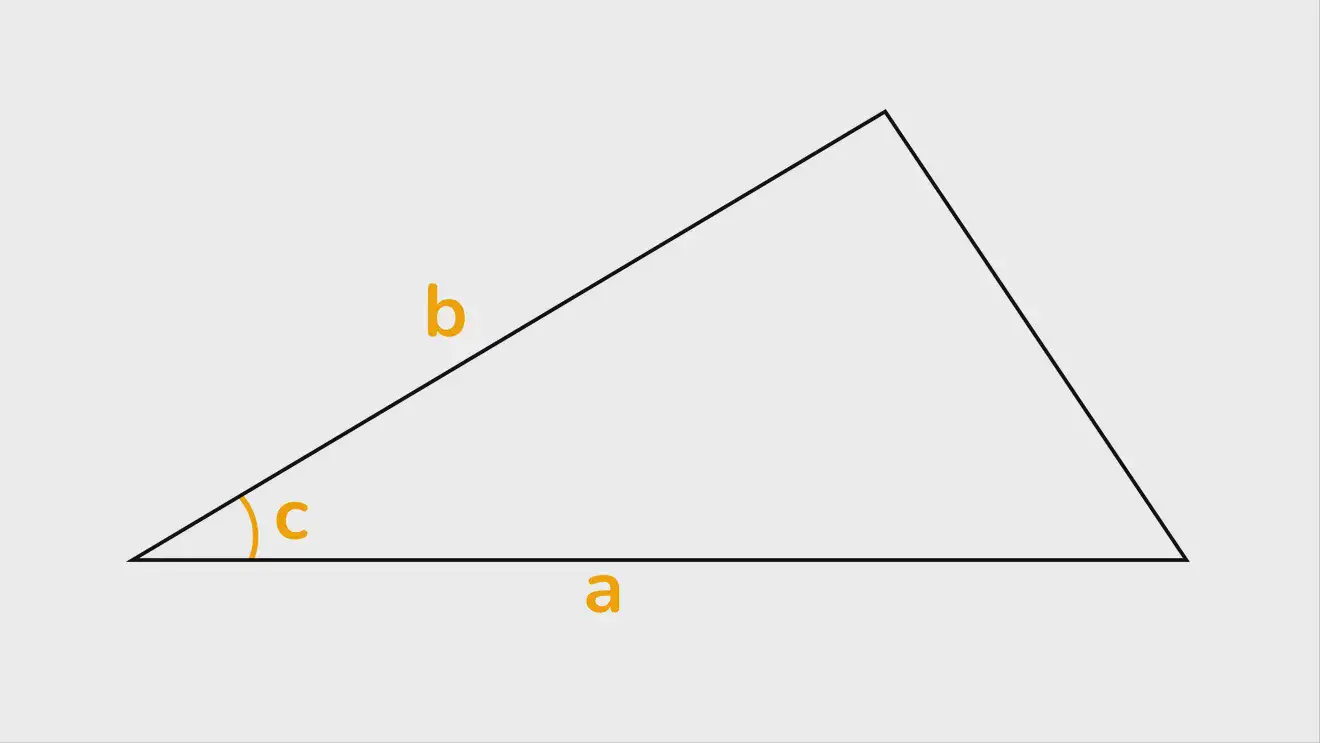
Если известны 2 любые стороны и угол между ними

Это вариант, подобный первому и второму. Здесь высота неизвестна, но есть длины 2 сторон и угол между ними. Определить высоту помогает значение sin для известного нам угла: это известная сторона, умноженная на синус угла b sin C, где C — величина угла.

И в целом S=1/2⋅a⋅b⋅sin C (a — длина стороны, от которой строилась высота).

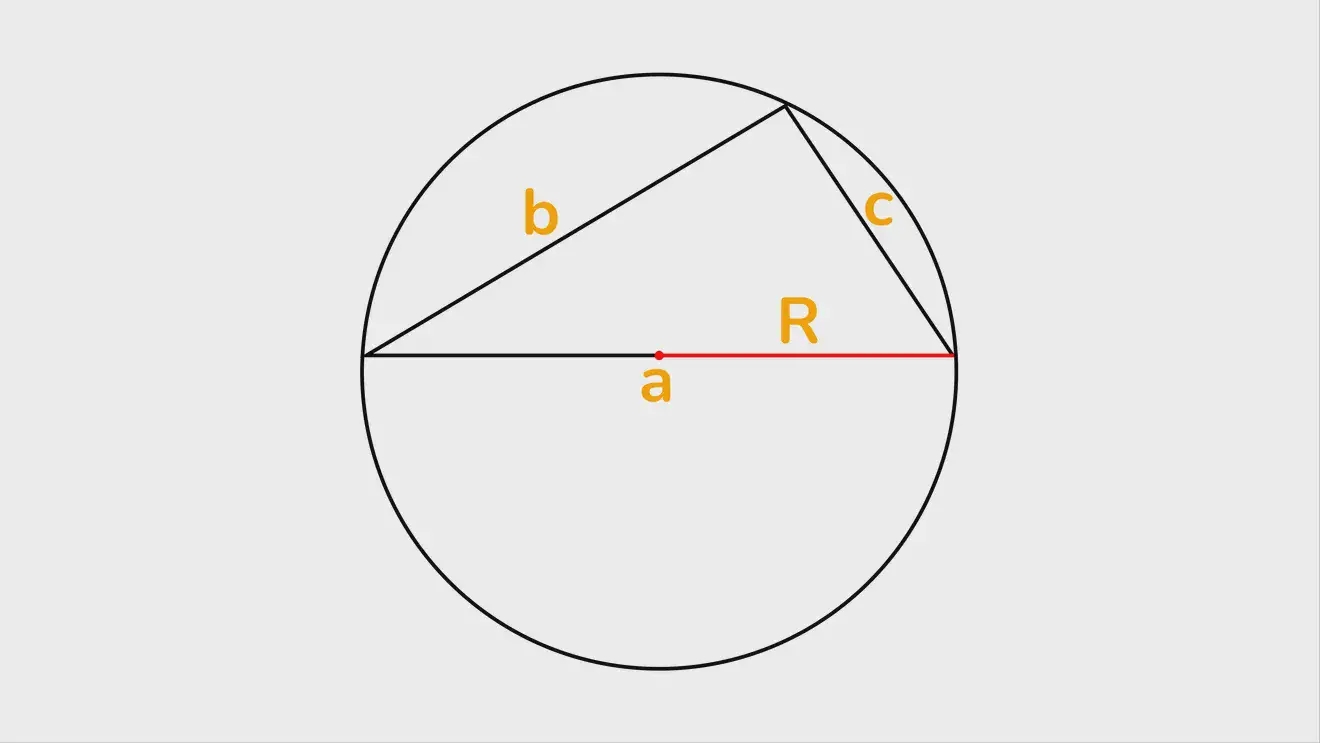
Если известны стороны треугольника и радиус описанной окружности

В отличие от предыдущего здесь неизвестен угол между сторонами, а точнее, значение его sin. Оно вычисляется с помощью вывода из теоремы синусов: для треугольника, вписанного в окружность, отношение любой стороны к синусу угла, расположенного напротив, равно удвоенному радиусу (r). Значит, sin нужного угла (С) равен длине стороны, поделённой на 2r.

То есть формула должна бы выглядеть S=1/2⋅a⋅b⋅с /2r, а если записать короче, будет S=a⋅b⋅с /4r (a, b и c — стороны треугольника).

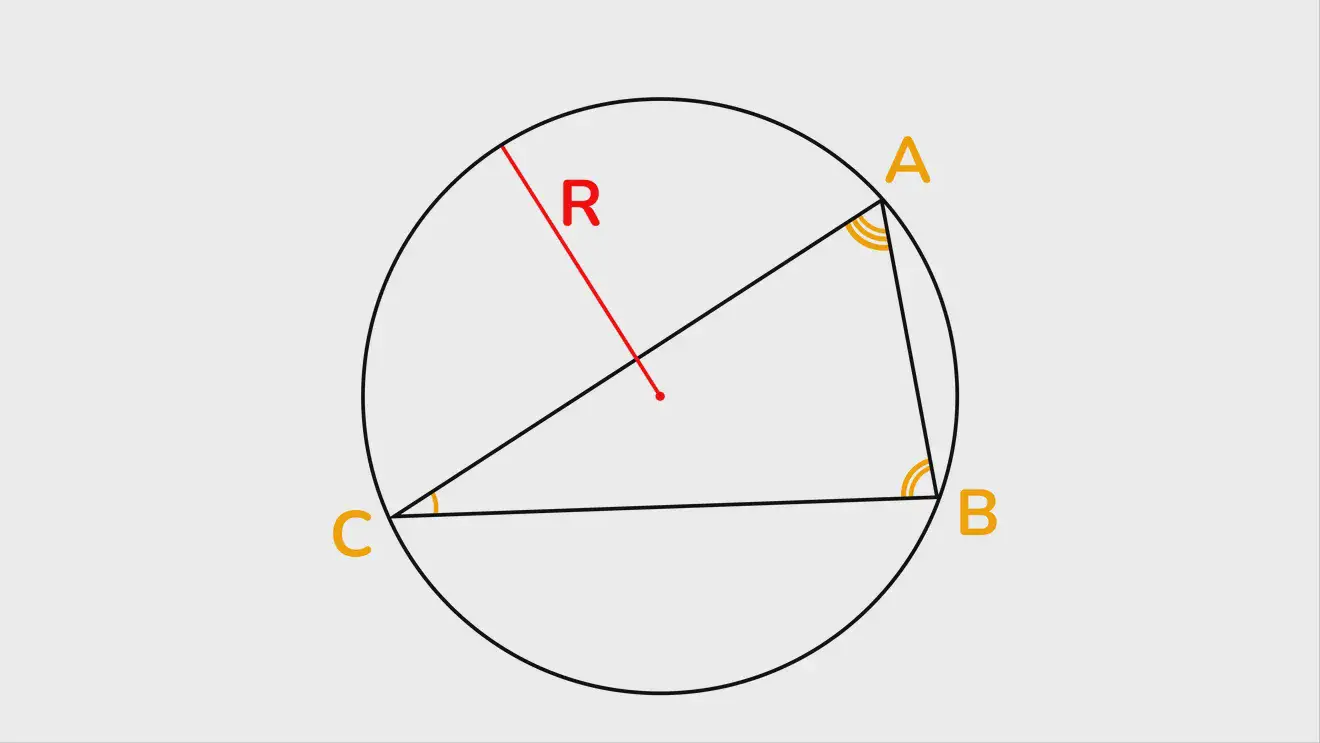
Если известны углы треугольника и радиус описанной окружности

Это частный случай применения упомянутого выше вывода теоремы синусов (про отношение сторон и синусов углов). Только сначала длина сторон вычисляется через sin углов.

S= 2r²⋅ sinA⋅sinB⋅sin C (r — радиус, A, B, C — углы).

Если известна одна сторона и прилежащие к ней 2 угла

Здесь логика та же самая: нахождение недостающего для известной формулы. Можно задействовать разные тригонометрические функции, и из-за этого конечный результат формально будет выглядеть по-разному:

S=a²⋅sinC⋅sinB/2 sin(C+B), если а — сторона, а C и B — прилежащие углы, или S=a ²/2(ctgB+ctgC) и т.д.

Формула Герона (если известны 3 стороны)

В её основе вариант 3 с использованием выводов теоремы косинусов и показателя p – суммы длин сторон треугольника, умноженной на ½ (т.е. полупериметра).

Вот итог: S= √(p(p — a)(p — b)(p — c)) (a, b и c — стороны треугольника).

Прямоугольные треугольники

Если известна гипотенуза (c) и один из острых углов (A), через его cos и sin можно получить длину катетов, т.е. S=1/2с²⋅cosA⋅sinA. Есть и другие варианты того же решения, например: S= с²⋅sin(2A)/4. 

Если известен один из катетов (a) и прилежащий к нему острый угол (B), длина второго катета определяется через tg острого угла. S= 1/2a ²⋅tgB.

Если известен противолежащий угол (А), меняется функция: S= 1/2a²⋅ctgA.

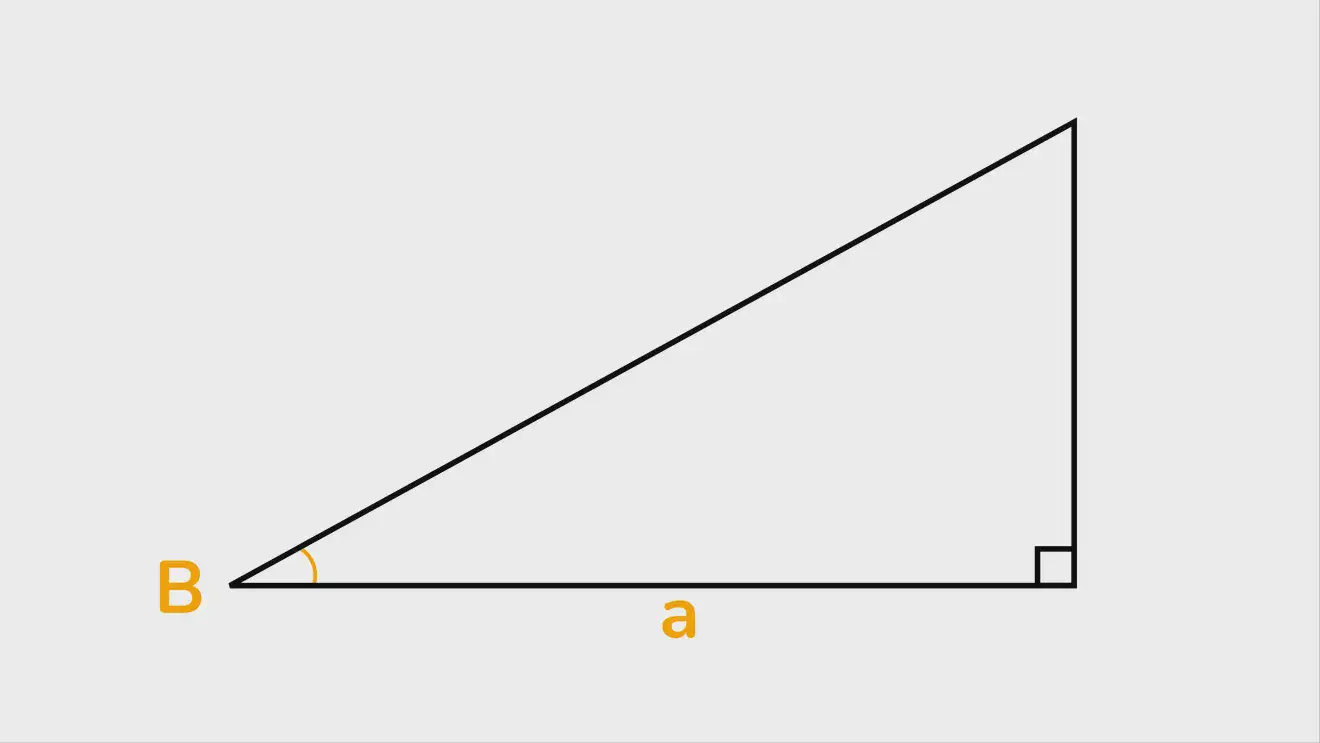
Равнобедренные и равносторонние треугольники

Особая формула для равнобедренного треугольника — это упрощённый вариант 3, когда известны 2 стороны и угол между ними. Из-за того, что 2 стороны равны, всё упрощается до половины произведения 3 величин: S=1/2 a²⋅sinB (где B — угол между равными сторонами a). В остальных случаях всё определяется подобно остальным типам треугольников.

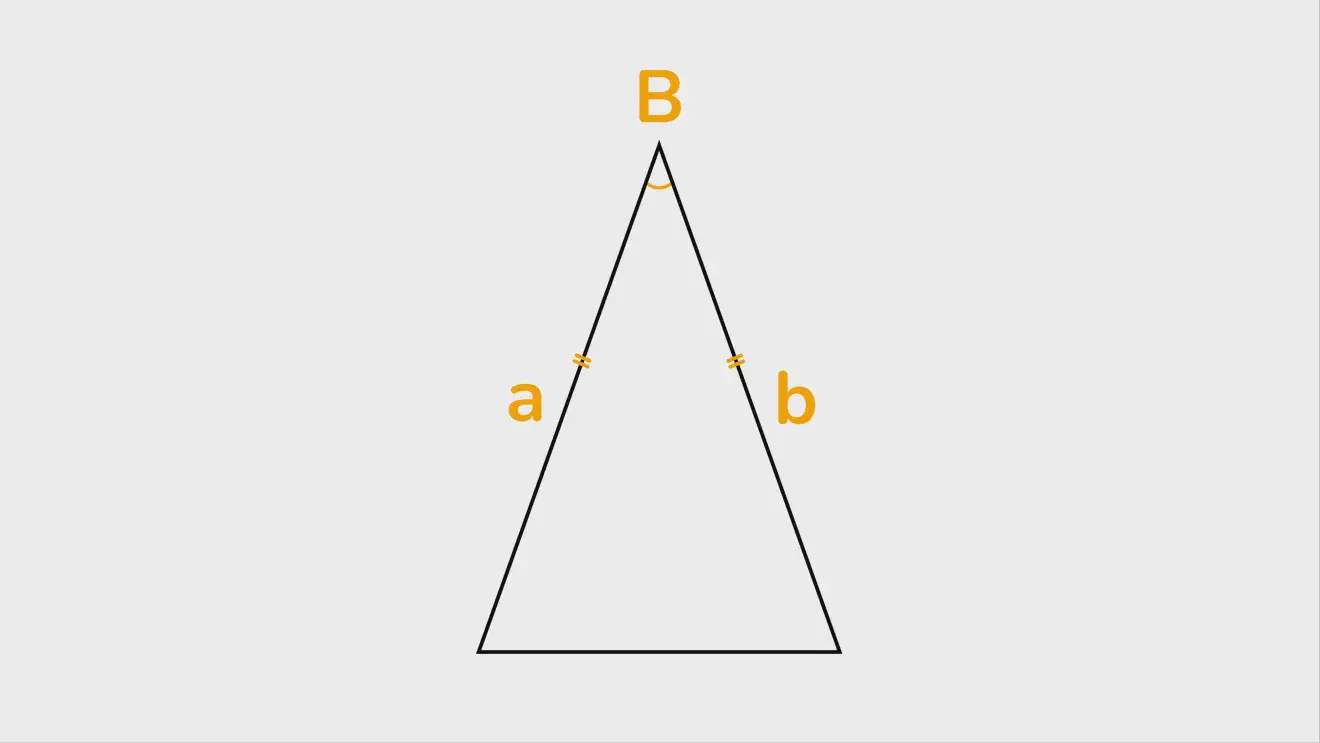
Для равностороннего треугольника с известной стороной (a) предыдущая формула дополнительно упрощается до S= ¼ a² √3.

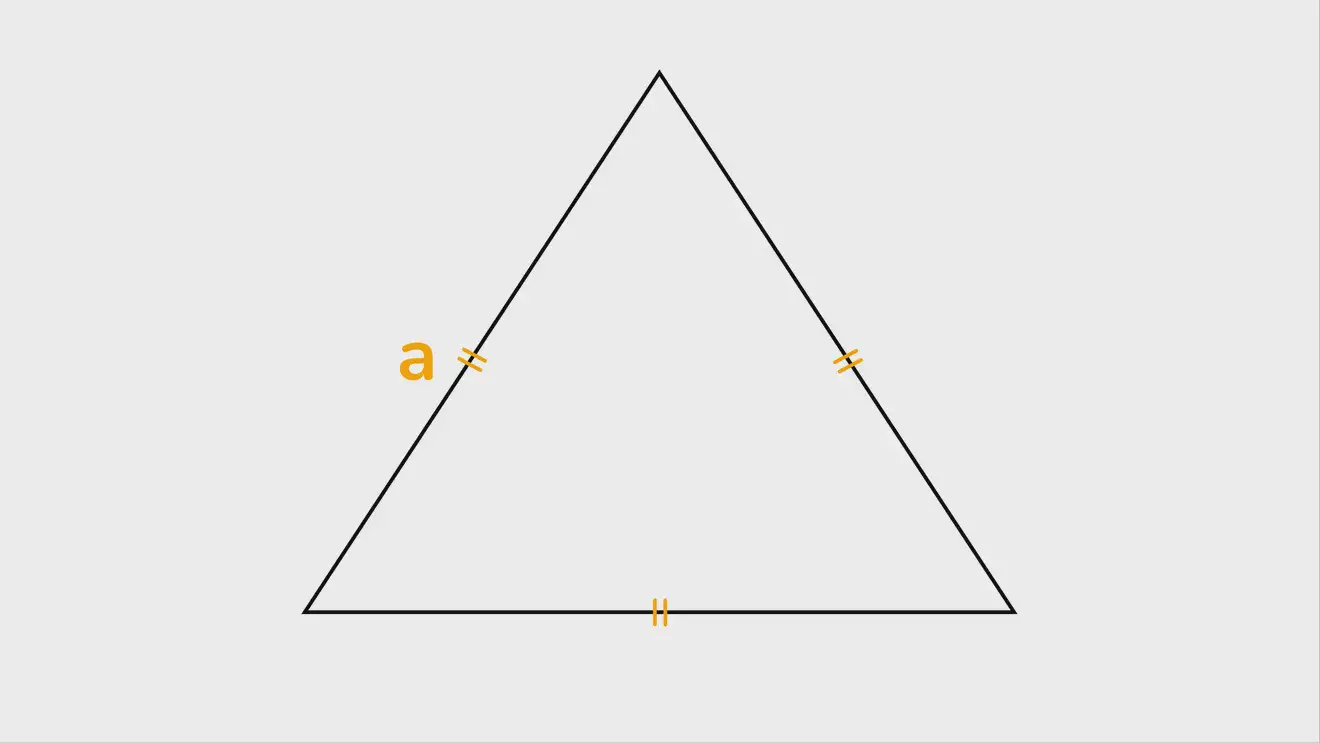
Для равностороннего треугольника с известной выcотой формула 1 также предельно упрощается:

S=h²/√3, либо S=h²√3/3

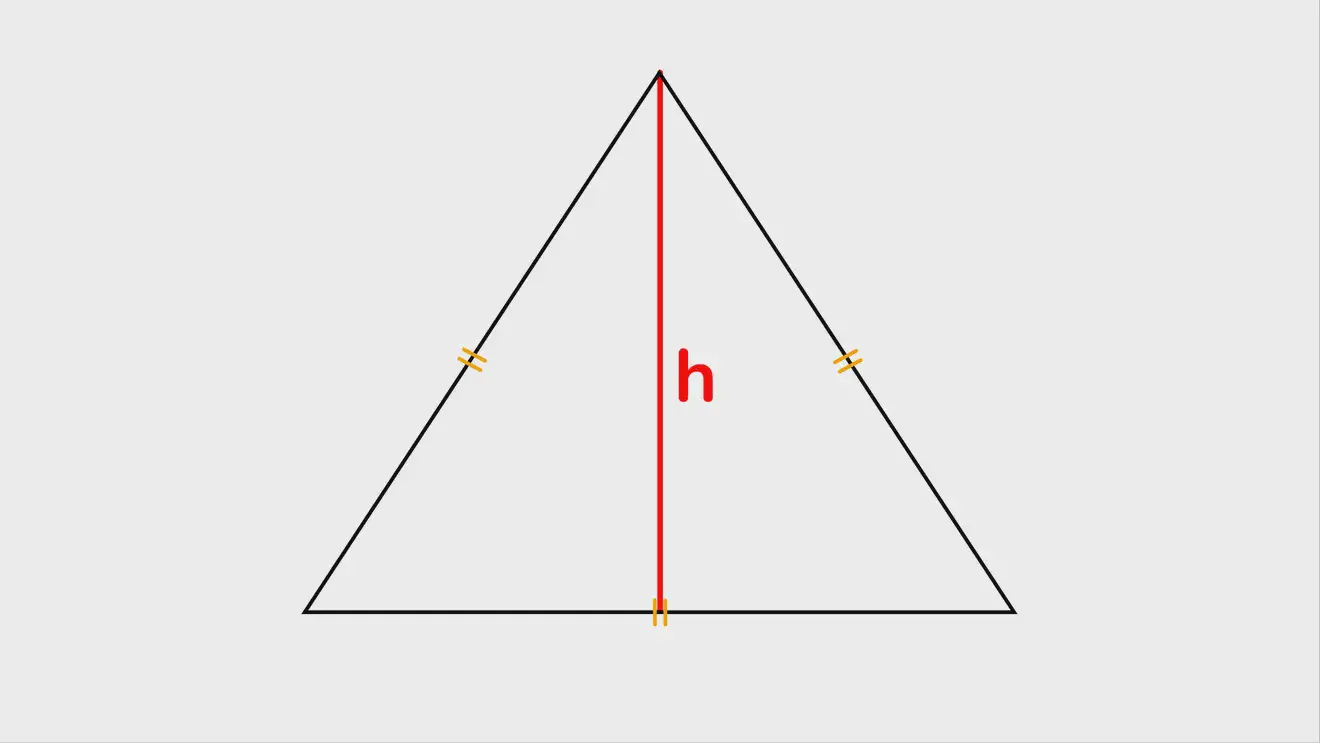
Площадь равностороннего треугольника через радиус вписанной и описанной окружности, соответственно: S=3√3r² (где r — радиус вписанной окружности) и S=1/4⋅3√3r² (где r — радиус описанной окружности).

Основные термины

Прямоугольный треугольник — треугольник, один из углов которого составляет 90°.

Равнобедренный прямоугольник — треугольник, 2 стороны которого равные по длине.

Равносторонний треугольник — треугольник, все стороны которого равные по длине, а все углы составляют 60°.

Катеты — 2 стороны прямоугольного треугольника, составляющие прямой угол.

Гипотенуза — сторона прямоугольного треугольника, противолежащая прямому углу.

Углы, прилежащие к стороне треугольника — те 2, через вершины которых проходит сторона.

Угол, противолежащий стороне — тот, через вершину которого сторона не проходит.

Примеры

(меры длины — см, мм и т.д. — для удобства не указываются)

• Дано: основание треугольника — 4, высота — 6. S = 1/2⋅a⋅h = S = 1/2⋅4⋅6 = 12.
• Дано: стороны треугольника — 8, 14 и 10, радиус вписанной окружности — 2.45. S = 1/2⋅r⋅(a+b+c) = 1/2⋅2.45⋅(8+14+10) = 39,2.
• Дано: стороны треугольника — 18 и 24, угол между ними 38°. S = 1/2⋅a⋅b sinC = 1/2⋅18⋅24 sin38° = 88,65.
• Дано: стороны треугольника — 8, 6 и 9, радиус описанной окружности — 4,59. S = a⋅b⋅с /4r = 8⋅6⋅9 /4⋅4,59 = 23,53.
• Дано: углы треугольника 46°, 60°, 74°, радиус описанной окружности — 5. S = 2r²⋅ sinA ⋅sinB⋅sinC = 2⋅25⋅0,72⋅0,87⋅0,96 = 30,01.
• Дано: стороны треугольника — 8, 14 и 10. p = (8+14+10)/2 = 16. S = √(p(p — a)(p — b)(p — c))= √(16(16 — 8)(16 — 14)(16 — 10)) = 39,2
• Дано: cторона — 18, прилежащие углы 46° и 64°. S=a²⋅sinC⋅sinB/2sin(C+B)=18²⋅0,72⋅0,9/2⋅0,94=111,67
• Дано: прямоугольный треугольник с гипотенузой 13 и прилежащим углом 76°. S=1/2с²⋅cosA⋅sinA = 13²⋅0,24⋅0,97/2 = 19,67
• Дано: равносторонний треугольник со стороной 5. S = ¼ a² √3 = ¼⋅25⋅1,73 = 10,8
• Дано: равносторонний треугольник с радиусом вписанной окружности 1,44. S = 3√3r² = 3⋅1,73⋅2,07 = 10,7

Материал был обновлён 08.11.2024