Вопреки наименованию «точная» наука, геометрия зачастую даёт нам не один и даже не два способа решения той или иной задачи. В качестве отличного примера такого обилия творческих подходов рассмотрим несколько вариантов вычисления радиуса окружности.
Через длину окружности
Для вычисления радиуса окружности через длину окружности необходимо знать следующую формулу:
Длина окружности = 2πr, где r — радиус окружности, а π — постоянное число, равное примерно 3,14.
Отсюда можно выразить радиус:
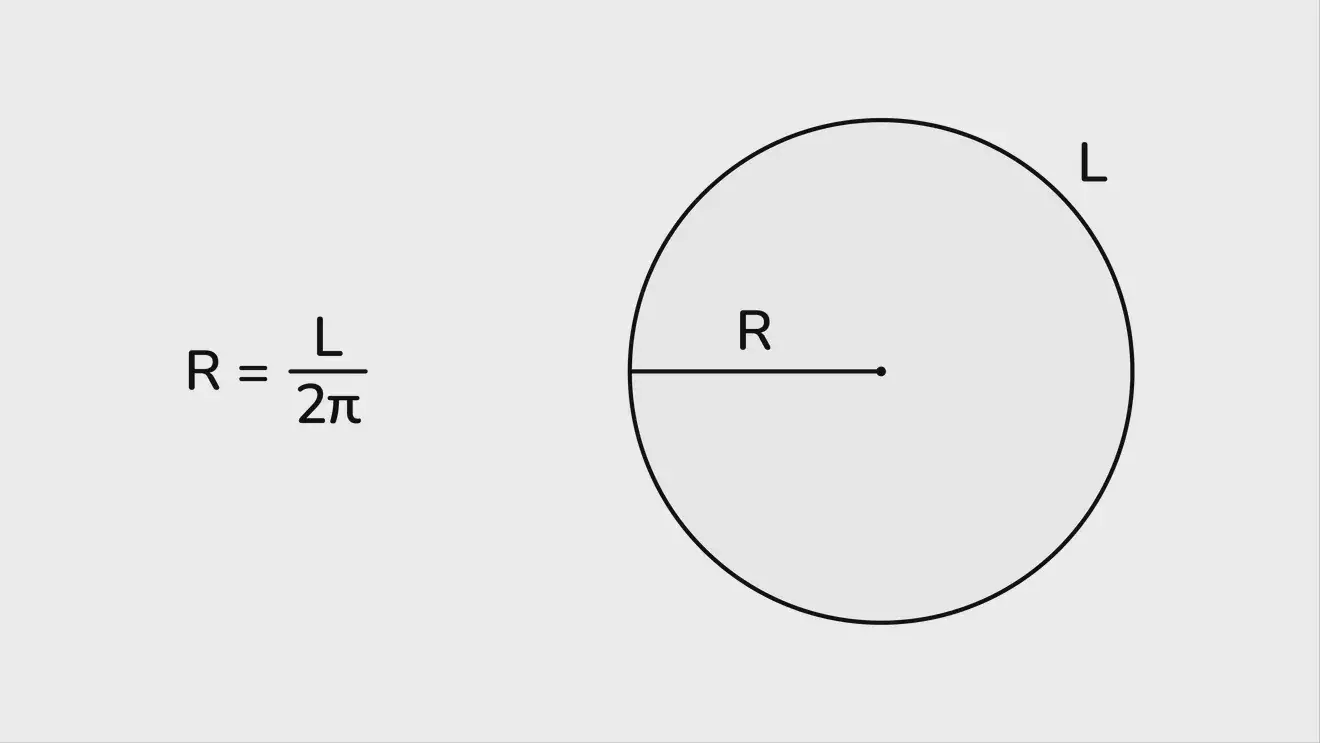
r = L / 2π, где L — длина окружности.
Соответственно, чтобы найти радиус окружности через длину окружности, нужно поделить длину окружности на 2π и получить результат.
Через диаметр окружности
Тут поможет простое правило: радиус равен половине диаметра.
При смене цвета осьминоги сжигают столько же калорий, сколько человек за 30 минут бегаОни тратят много сил маскировкуПолучается, если нам известен диаметр (обозначается буквой d), то радиус (обозначается буквой r) можно найти по формуле:
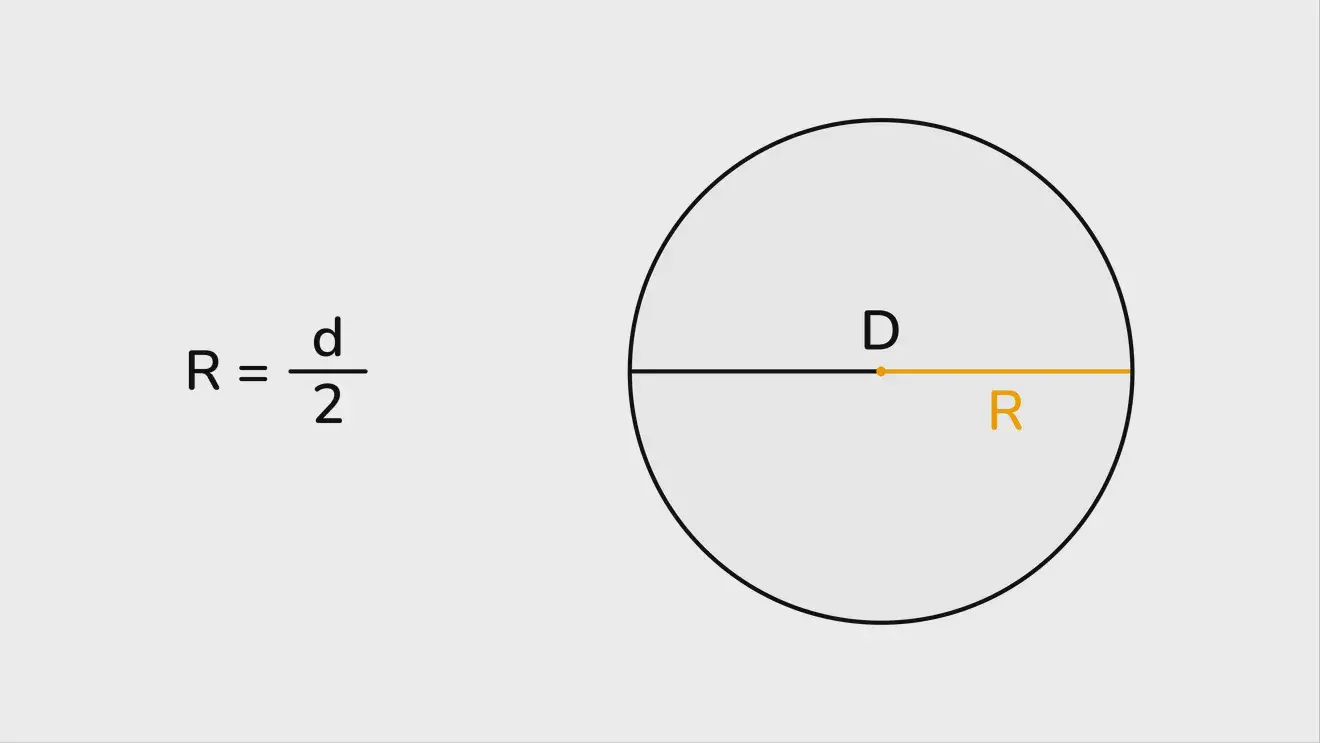
r = d / 2, где d — диаметр окружности.
Через стороны и площадь вписанного треугольника
Для этого метода вам понадобится использовать формулу Герона для вычисления площади треугольника и формулу радиуса окружности:
S = p(p-a)(p-b)(p-c), где p = (a+b+c)/2, a, b, c — стороны треугольника
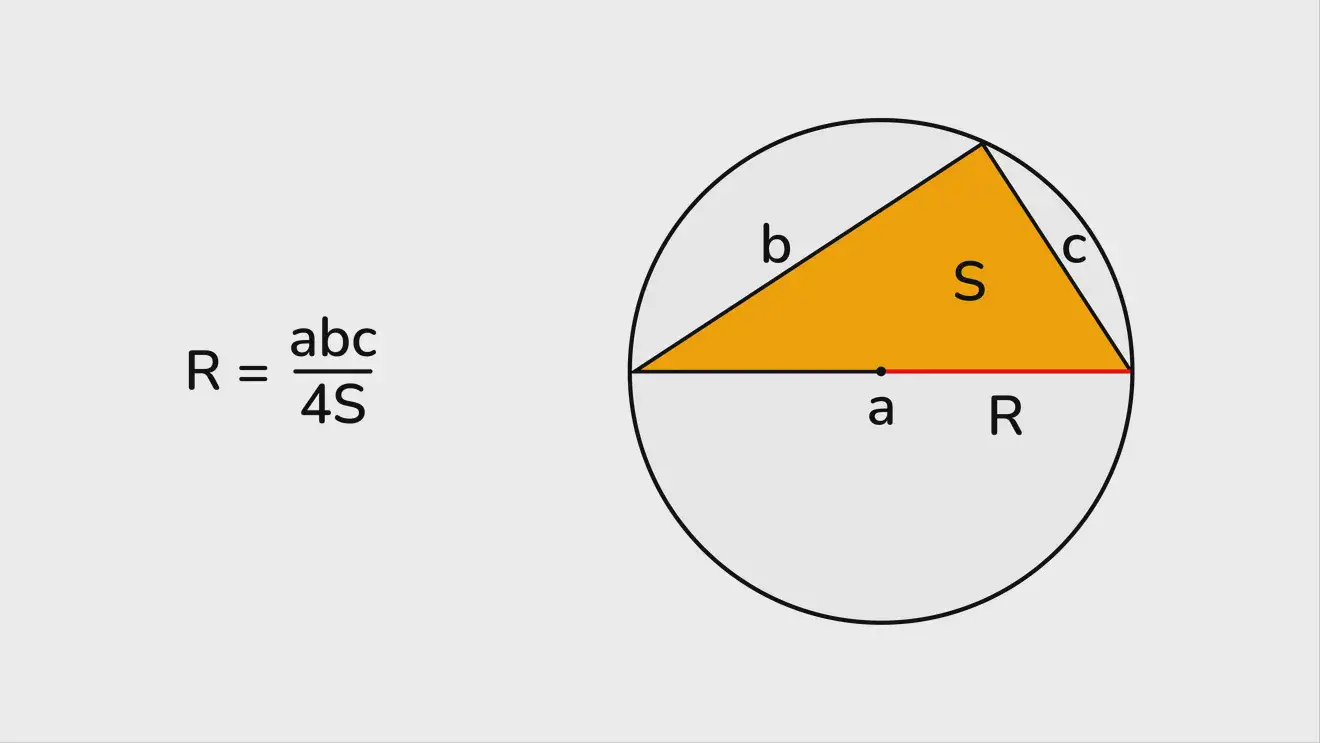
R = abc / (4S), где a, b, c - стороны треугольника, S — площадь треугольника
Через площадь описанного треугольника
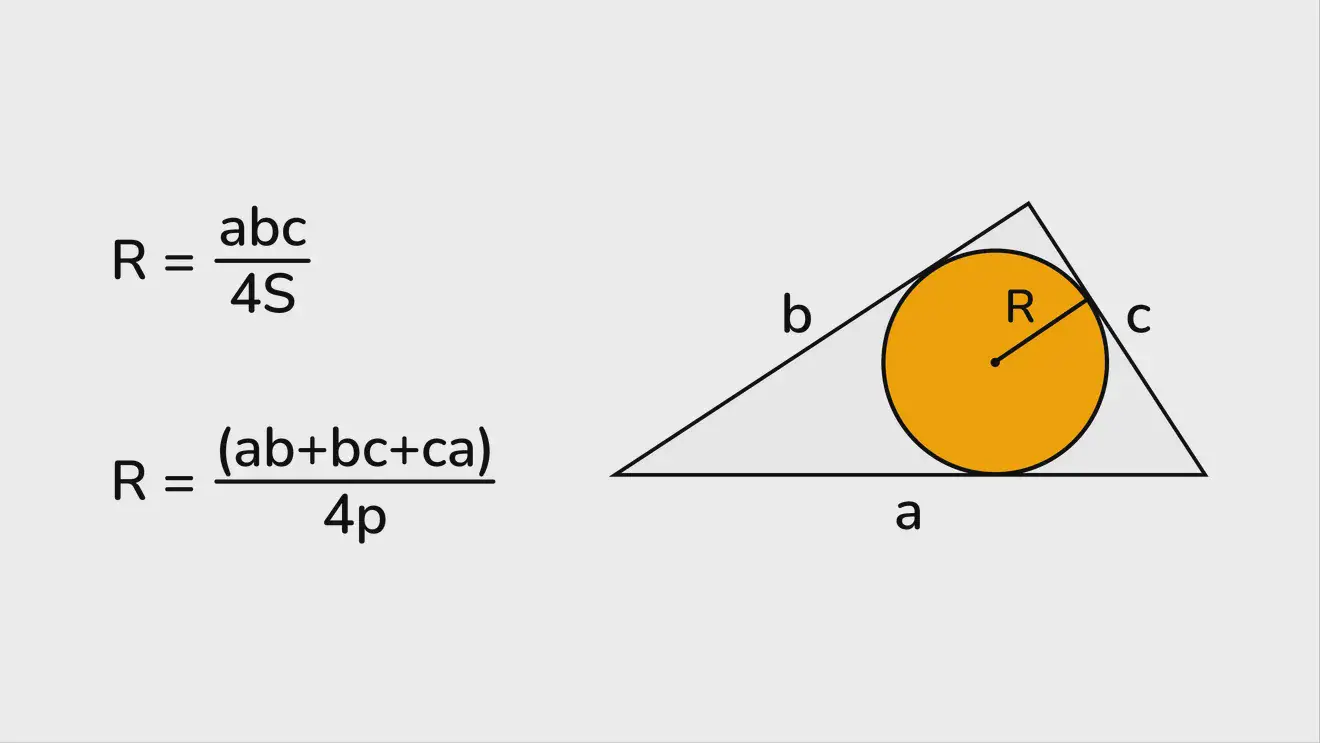
Чтобы найти радиус окружности через площадь и полупериметр описанного треугольника, можно использовать следующую формулу:
R = abc/4S, где a, b, c — стороны треугольника, S — его площадь, а R — радиус описанной окружности. Если известен полупериметр p = (a+b+c)/2, то можно выразить радиус через полупериметр и площадь:
Через диагональ описанного квадрата
Чтобы найти радиус окружности через сторону описанного квадрата, нужно запомнить, что радиус окружности равен половине диагонали квадрата.
Сторона описанного квадрата (a) и его диагональ (d) связаны соотношением:
d = a√2
Тогда радиус описанной окружности будет равен:
R = d/2 = a√2 / 2
